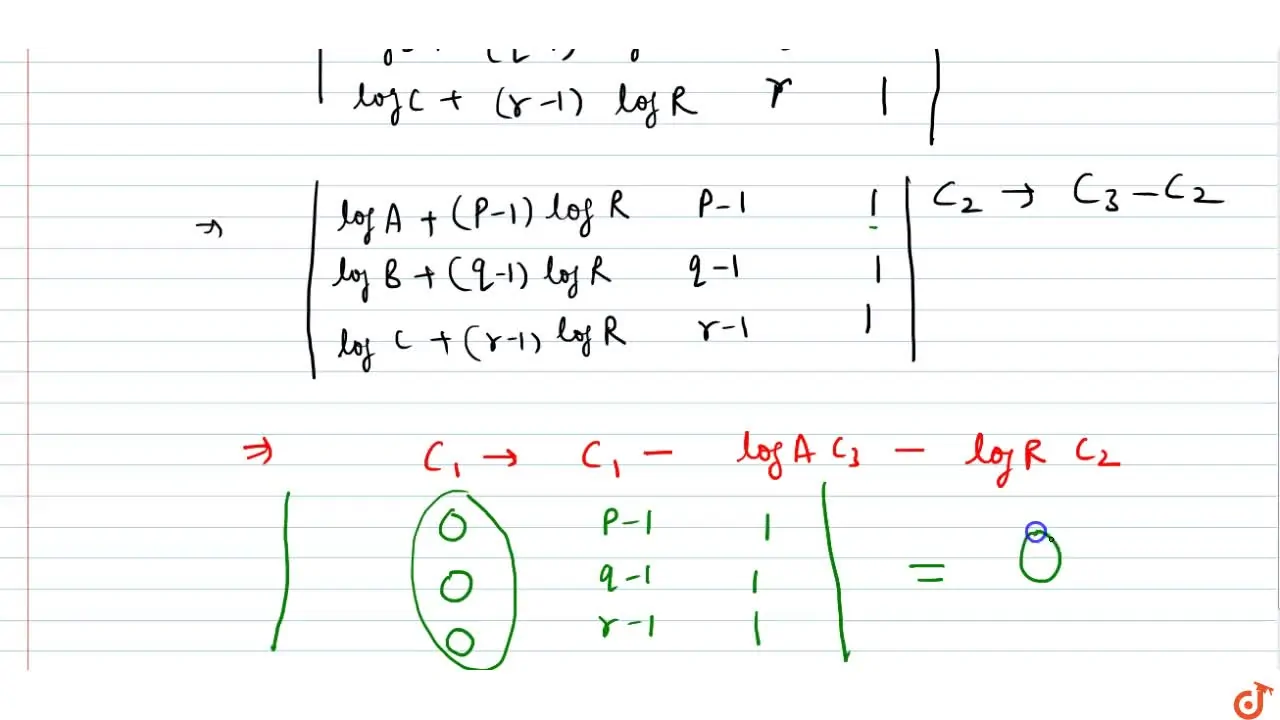If a,b,c are all positive and are pth,qthandrth terms of a G.P., then that =|logap1logbq1logcr1|=0
a→pth
b→qth
c→rth
a=ARP−1
b=ARq−1
c=ARr−1
loga=logA+(p−1)logR
logb=logA+(q−1)logR
logc=logA+(r−1)logR
⇒∣∣
∣
∣∣logA+(p−1)logRp1logB+(q−1)logRq1logC+(r−1)logRr1∣∣
∣
∣∣
C2→C3−C2
=∣∣
∣
∣∣logA+(p−1)logRp−11logB+(q−1)logRq−11logc+(r−1)logRr−11∣∣
∣
∣∣
C1→C1−logAC3−logRC2
∣∣
∣
∣∣0p−110q−110r−11∣∣
∣
∣∣=0
Answer
Related Playlists
Similar Questions
If a,b,c are positive and are the pth, qth and rth terms respectively of a G.P., the the value of ∣∣ ∣ ∣∣logap1logbq1logcr1∣∣ ∣ ∣∣= (A) 1 (B) pqr(loga+logb+logc) (C) 0 (D) apbqcr
View SolutionIf a,b,c are positive and ar the pth,qth,rth terms respectively of a G.P show that, ∣∣ ∣ ∣∣logap1logbq1logcr1∣∣ ∣ ∣∣=0
View SolutionIf a,b,and c are positive and are the pth, qth and rth terms respectively of a GP. Show without expanding that
∣∣ ∣ ∣∣logap1logbq1logcr1∣∣ ∣ ∣∣=0View SolutionIf a>0,b>0,c>0 are respectively the pth , qth , rth terms of G.P., then value of the determinant ∣∣ ∣ ∣∣logap1logbq1logcr1∣∣ ∣ ∣∣ is
View SolutionIf a,b,c are respectively the xth, yth and zth terms of a G.P. then the value of
(y−z)loga+(z−x)logb+(x−y)logc:View SolutionIf the positive numbers a, b and c are the pth, qth and rth terms of GP, then the vectors (loga)ˆi+(logb)ˆj+(logc)ˆkand(q−r)ˆi+(r−p)ˆj+(p−q)ˆk are
View SolutionIf a,b,c are respectively the pth , qth and rth terms of an H.P. then
∣∣ ∣ ∣∣bccaabpqr111∣∣ ∣ ∣∣ =View SolutionSuppose a,b,c>0 and are respectively the pth, qth and rth terms of a G.P. Let
x=(loga)i+(logb)j+(logc)k
y=(q−r)i+(r−p)j+(p−q)k
If angle between x and y is kπ, then k = ______View Solutionl, m,n are the pth,qthandrth term of a G.P. all positive, then ∣∣ ∣ ∣∣loglp1logmq1lognr1∣∣ ∣ ∣∣ equals :
View SolutionIf a,b,c are respectively the pth,qthandrth terms of a G.P. show that (q−r)loga+(r−p)logb+(p−q)logc=0.
View Solution