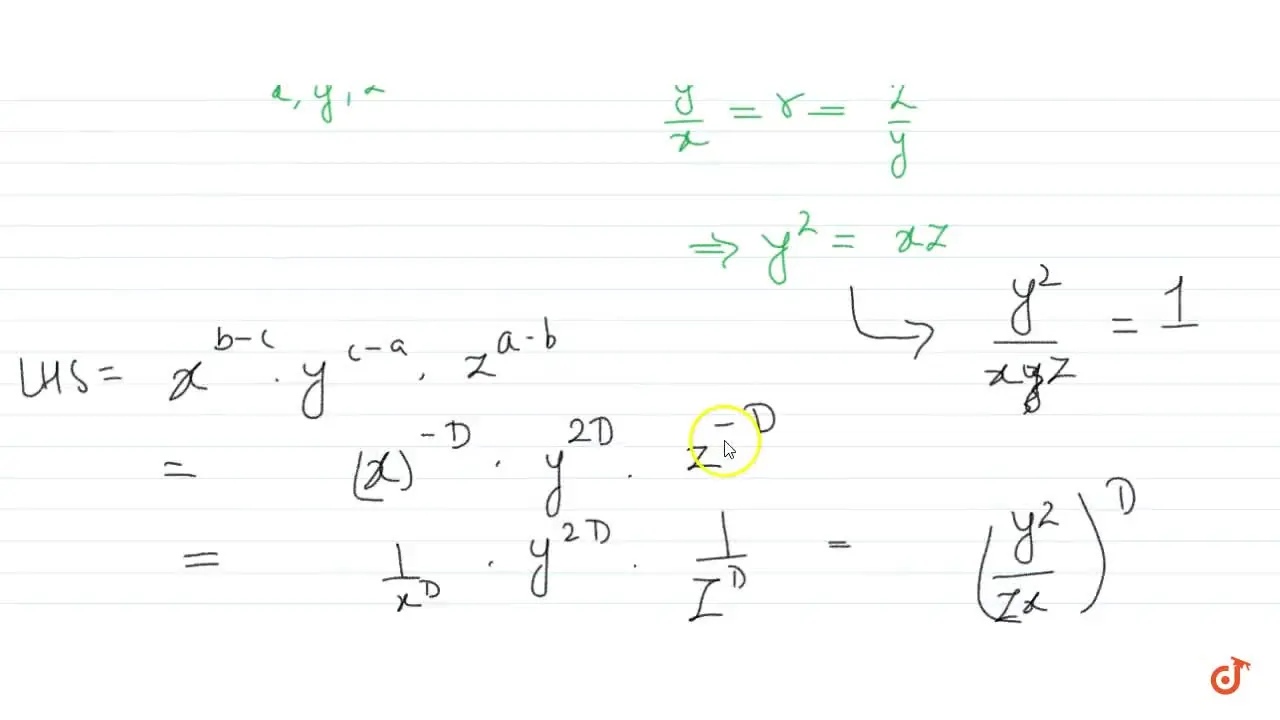If a,b,c,d are in A.P. and x,y,z are in G.P., then show that xb−c.yc−a.za−b=1.
Video Solution
Text Solution
Let D is the common difference in the given A.P.
Then,
b−a=D,c−b=D,d−c=D
∴b−c=−D,c−a=2D,a−b=−D
As, x,yandz are in G.P.
∴y2=zx
Now, xb−c⋅yc−a⋅za−b=x−D⋅y2D⋅z−D
=(1zx)D⋅(y2)D
=(y2zx)D
=(zxzx)D...[As y2=zx]
=1D=1
∴xb−c⋅yc−a⋅za−b=1
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If a,b,c,d are in A.P. and x,y,z are in G.P., then show that xb−c.yc−a.za−b=1.
View SolutionIf a, b, c are in A.P. and x, y, z are in G.P., then prove that :
xb−c.yc−a.za−b=1View SolutionIf a, b, c are in A.P. and b-a, c-b, a are in G.P. then a:b:c=?
View SolutionIf a, b, c are in A.P. and b-a, c-b, a are in G.P. then a:b:c=?
View SolutionIf a, b, c are in A.P. and b-a, c-b, a are in G.P. then a:b:c=?
View SolutionIf a,b, and c are in A.P and b-a,c-b and a are in G.P then a:b:c is
View SolutionIf a,b,c are in A.P. and x,y,z in G.P., prove that xb−c.yc−a.za−b=1
View SolutionIf x, y ,z are in G.P. and ax=by=cz , then :
View SolutionIf a,b,c are in A.Panda,b,d are in G.P, prove that a,a−b,d−c are in G.P.
View SolutionIf a, b, c are in A.P. and a, x, b, y, c are in G.P., then prove that b2 is the arithmatic mean of x2 and y2.
View Solution