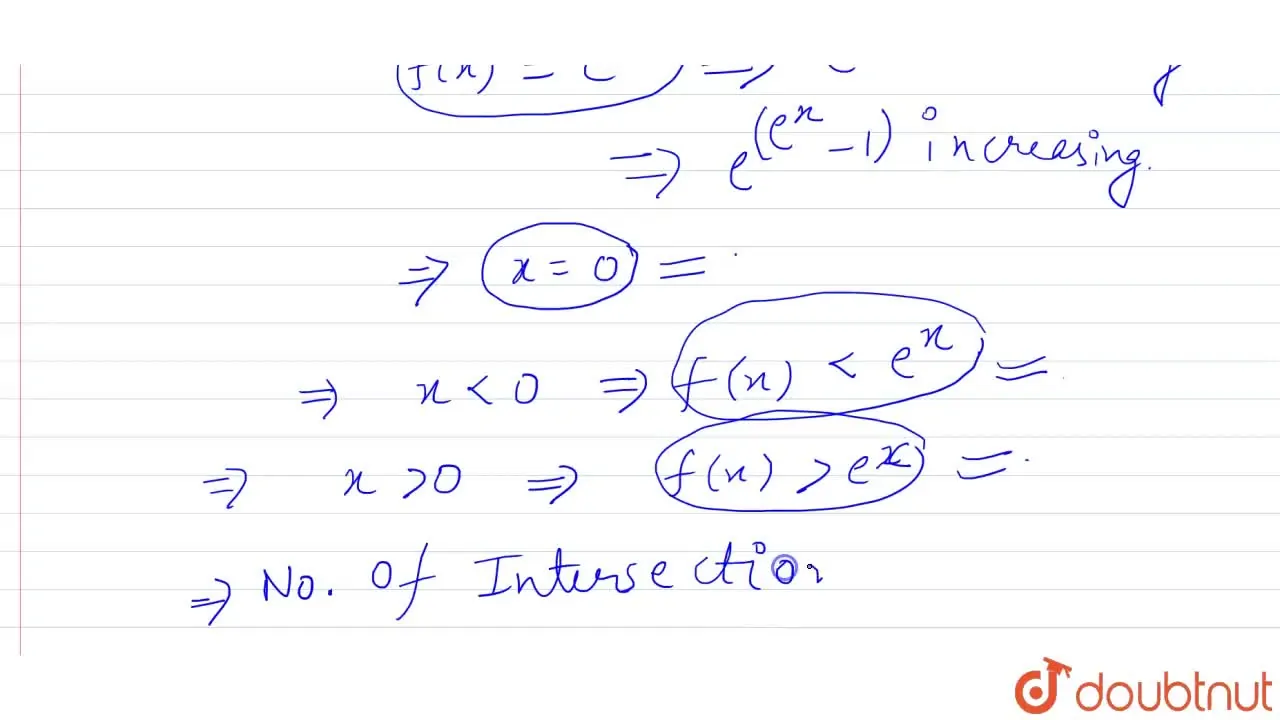If a function satisfies the relation f(x)f''(x)−f(x)f'(x)=(f'(x))2∀x∈Randf(0)=f'(0)=1, then
Number of roots of the equation f(x)=ex is
0
1
2
infinite
The correct Answer is:B
f(x)f''(x)−f(x)f'(x)=(f'(x))2
∴f''(x)−f'(x)f'(x)=f'(x)f(x)
⇒f''(x)f'(x)−1=f'(x)f(x)
On integrating both sides w.r.t. x, we get
loge(f'(x))−x=logef(x)+c
f(0)=f'(0)=1
∴0−0=0+c
∴c=0
∴loge(f'(x))−x=logef(x)
⇒loge(f'(x))−logef(x)=x
⇒f'(x)f(x)=ex
On integrating both sides w.r.t. x. we get
∴logef(x)=ex+c
Putting x=0, we get c=−1
∴logef(x)=ex−1
∴f(x)=eex−1
Related Playlists
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Matrix)4videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Numerical)10videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Multiple)17videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
Similar Questions
If a function satisfies the relation f(x)f''(x)−f(x)f'(x)=(f'(x))2∀x∈Randf(0)=f'(0)=1, then
The value of limx→−∞f(x) isView SolutionIf a function 'f' satisfies the relation f(x)f''(x)−f(x)f′(x)−f′(x)2=0∀x∈R and f(0)=1=f′(0). Then find f(x).
View SolutionThe function f(x) satisfying the equation f2(x)+4f'(x)f(x)+(f'(x))2=0
View SolutionA function f(x) satisfies the relation f(x+y)=f(x)+f(y)+xy(x+y),∀x,y∈R. If f'(0) = - 1, then
View SolutionIf function f satisfies the relation f(x)⋅f′(−x)=f(−x)⋅f′(x) for all x ,and f(0)=3, and if f(3)=3, then the value of f(−3) is ______________
View SolutionIf f satisfies the relation f(x+y)+f(x−y)=2f(x)f(y)∀x,y∈Kandf(0)≠0; then f(10)−f(−10)−
View SolutionLet f be a differentiable function satisfying f'(x)=2f(x)+10∀x∈Randf(0)=0, then the number of real roots of the equation f(x)+5sec2x=0 ln (0,2π) is:
View SolutionFunction f satisfies the relation f(x)+2f(11−x)=x∀x∈R−{1,0} then f(2) is equal to
View SolutionThe function f(x) satisfy the equation f(1−x)+2f(x)=3x∀x∈R, then f(0)=
View SolutionIf a function f(x) satisfies the relation 3f(x)−5f(2x)=3−x+x2∀x∈R−{0} ,then the value of f(1) is equal to
View Solution