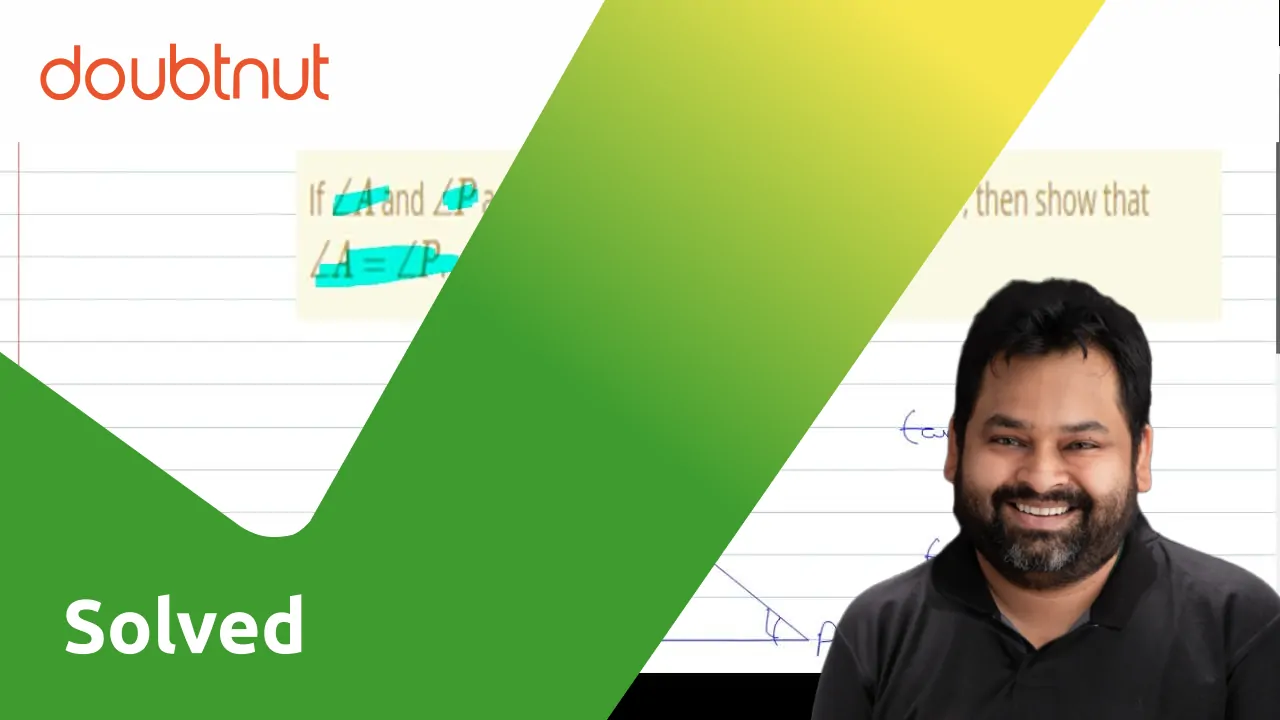
If ∠A and ∠P are acute angle such that tanA=tanP, then show that ∠A=∠P.
Video Solution
Text Solution
Let we create a right angle triangle ABP with the given details.
Please refer to video to see the triangle.
Then,
tanA=BPAB
tanP=ABBP
It is given,
tanA=tanP
∴BPAB=ABBP
⇒BP2=AB2
⇒BP=AB
We know, opposite angles of equal sides are also equal.
∴∠A=∠P
Was this answer helpful?606
Updated on:21/07/2023
Similar Questions
∠P and ∠Q are supplementary angles. If ∠P=∠Q−40∘, then find ∠P and ∠Q.
03:20View SolutionIn △ABCand△PQR,AB=PQ,∠A=∠P and ∠B=∠Q. If ∠A+∠C=130∘, then ∠Q = ..........
01:36View Solution∠P and ∠Q are supplementary angles. If ∠P=∠Q−40∘, find ∠P and ∠Q
02:40View SolutionIn △ABCand△PQR,AB=PQ,∠A=∠P and ∠B=∠Q. If ∠A+∠C=130∘, then ∠Q = ..........
02:10View Solutionif ∠A and ∠B are acute angles such that cos A = cos B , show that ∠A=∠B .
03:23View Solutionयदि ∠A=∠P,∠B=∠Q औरAB=PQ तो-
01:16View SolutionABCD is a parallelogram. Angle bisector of ∠A and angle bisector of ∠C cuts extended side DC and AB at Q and P respectively. If ∠A=50∘, find ∠P+∠Q.
02:38View SolutionFind ∠A+∠B+∠C+∠P+∠Q+∠R.
 02:06View Solution
02:06View Solution