If d1,d2 (d_2>d_1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle prove that d22=c2+d21
The correct Answer is:d22=C2−d21
Step by step video, text & image solution for If d_1,d_2 (d_2>d_1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle prove that d_2^2=c^2+d_1^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - SHORT ANSWER TYPE - II QUESTIONS
4 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS
2 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - D)
1 Videos
- ARITHMETIC PROGRESSION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)
1 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D
1 Videos
Similar Questions
If d1,d2 (d_2>d_1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle prove that d22=c2+d21
View SolutionIf radii of the two concentric circles are 15cm and 17cm, then the length of each chord of one circle which is tangent to other is: 8cm (b) 16cm (c) 30cm (d) 17cm
View Solution
Knowledge Check
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cm
lf D is thedaneter of the brger circle and d the diameter of the small circle then D+d=?
View SolutionIn the following diagram four circles are tangent to every other circle. The radius of each of the circles A,B and C is 1. Find the radius of circle D, which is tangent to all the three given circles and lies at the centre.

View SolutionIf the diagram, DC is a diameter of the large circle centered at A, and AC is a diameter of the smaller circle centered at B. If DE is tangent to the smaller circle at F and DC=12 then the length of DE is
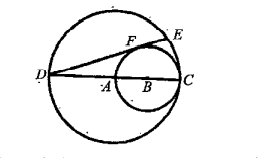 .
.
View SolutionIf the circumference and the area of a circle are numerically equal, then diameter of the circle is (a) π2 (b) 2π (c) 2 (d) 4
View SolutionA line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is 2d1+d22 (b) d1+2d22 d1+d2 (d) d1d2d1+d2
View SolutionIf the length of the chord of the circle x2+y2=4 through (1,12) which is of minimum length is d, find d2.
View Solution
