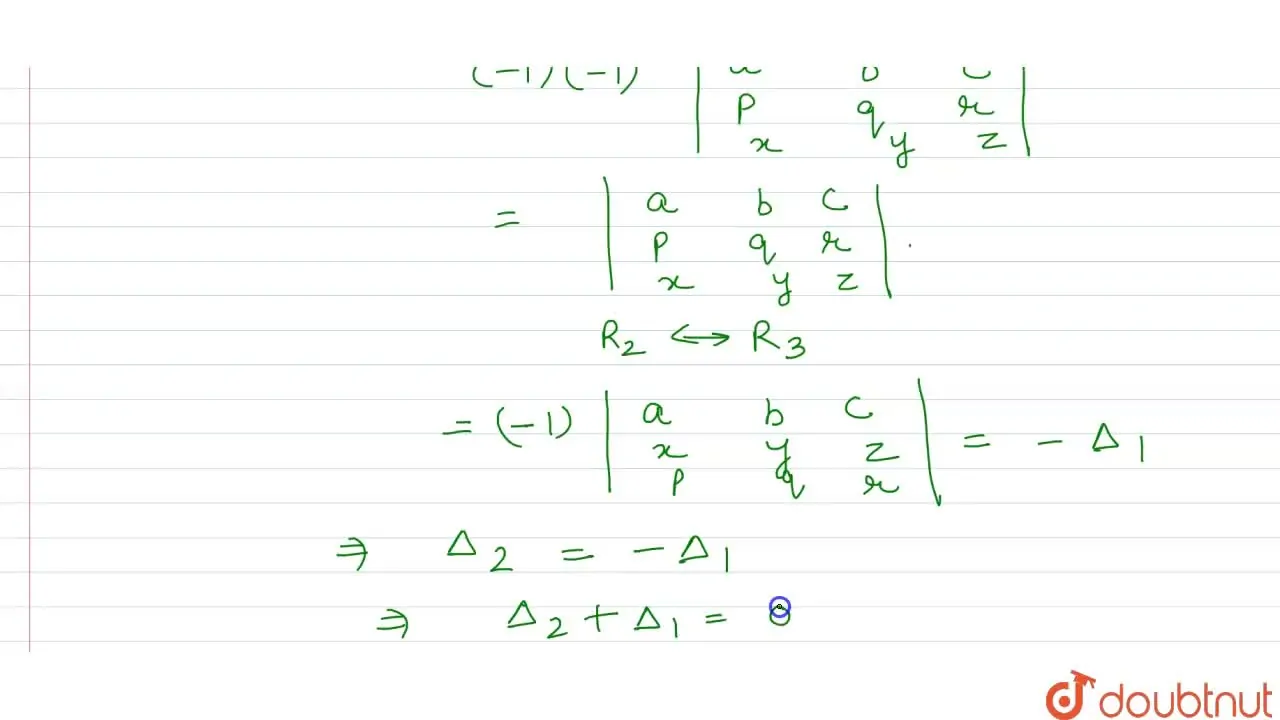If Δ1=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣and Δ2∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣ then without expanding Δ1 and Δ2,prove that Δ1+Δ2=0
We have
Δ2=∣∣
∣
∣∣q−by−pa−xr−cz∣∣
∣
∣∣
=(−1)⋅∣∣
∣
∣∣q−byp−axr−cz∣∣
∣
∣∣[taking (-1) common fromR2]
=(−1)(−1)⋅∣∣
∣
∣∣qbypaxrcz∣∣
∣
∣∣[taking (-1) common fromC2]
=∣∣
∣
∣∣qbypaxrcz∣∣
∣
∣∣=∣∣
∣
∣∣qprbacyxz∣∣
∣
∣∣[interchanging rows and columns]
=(−1)∣∣
∣
∣∣pqrabcxyz∣∣
∣
∣∣[applyingC1↔C2]
=(−1)(−1)⋅∣∣
∣
∣∣abcpqrxyz∣∣
∣
∣∣[applyingR1↔R2]
=∣∣
∣
∣∣abcpqrxyz∣∣
∣
∣∣
=(−1)⋅∣∣
∣
∣∣abcxyzpqr∣∣
∣
∣∣=−Δ1[applying R2↔R3]
Thus, Δ2=−Δ1andhenceDelta_(1) + Delta_(2) =0
Related Playlists
- BOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Exercise 6A22videos
DETERMINANTS
- BOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Exercise 6B44videos
DETERMINANTS
- BOOK - RS AGGARWALCHAPTER - DEFINITE INTEGRALSEXERCISE - Objective Questions73videos
DEFINITE INTEGRALS
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18C16videos
DIFFERENTIAL EQUATIONS AND THEIR FORMATION
Similar Questions
If Δ1=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣ and Δ2=∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣, without expending or evaluating Δ1andΔ2 , show that Δ1+Δ2=0
View SolutionIf Δ1=∣∣ ∣ ∣∣111x2y2z2xyz∣∣ ∣ ∣∣ and Δ2=∣∣ ∣ ∣∣111yzzxxyxyz∣∣ ∣ ∣∣ then without expanding show that Δ1=Δ2
View SolutionIf Δ1=∣∣ ∣∣xbbaxbaax∣∣ ∣∣ and Δ2=∣∣∣xbax∣∣∣, then
View SolutionIf Δ1=∣∣ ∣∣xabbxaabx∣∣ ∣∣andΔ2=∣∣∣xbax∣∣∣ are the given determinants then
View SolutionIf Δ1=∣∣ ∣ ∣∣2abe2def4x2y2z∣∣ ∣ ∣∣,Δ2=∣∣ ∣ ∣∣f2de2z4x2ye2ab∣∣ ∣ ∣∣, then the value of Δ1−Δ2 is
View Solution" 1."|[a-b,b-c,c-a],[x-y,y-z,z-x],[p-q,q-r,r-p]|" is equal to "
View SolutionIf Δ1=∣∣ ∣∣xbbaxbaax∣∣ ∣∣ and Δ2=∣∣∣xbax∣∣∣ are the given determinants then
View SolutionIf Δ1=∣∣ ∣ ∣∣111abca2b2c2∣∣ ∣ ∣∣,Δ2=∣∣ ∣∣1bca1cab1abc∣∣ ∣∣, then
View SolutionWithout expanding evaluate the determinant Delta=∣∣ ∣ ∣∣111abca2b2c2∣∣ ∣ ∣∣ .
View SolutionProve that: ∣∣ ∣ ∣∣b+cc+aa+bq+rr+pp+qy+zz+xx+y∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣abcpqrxyz∣∣ ∣ ∣∣
View Solution