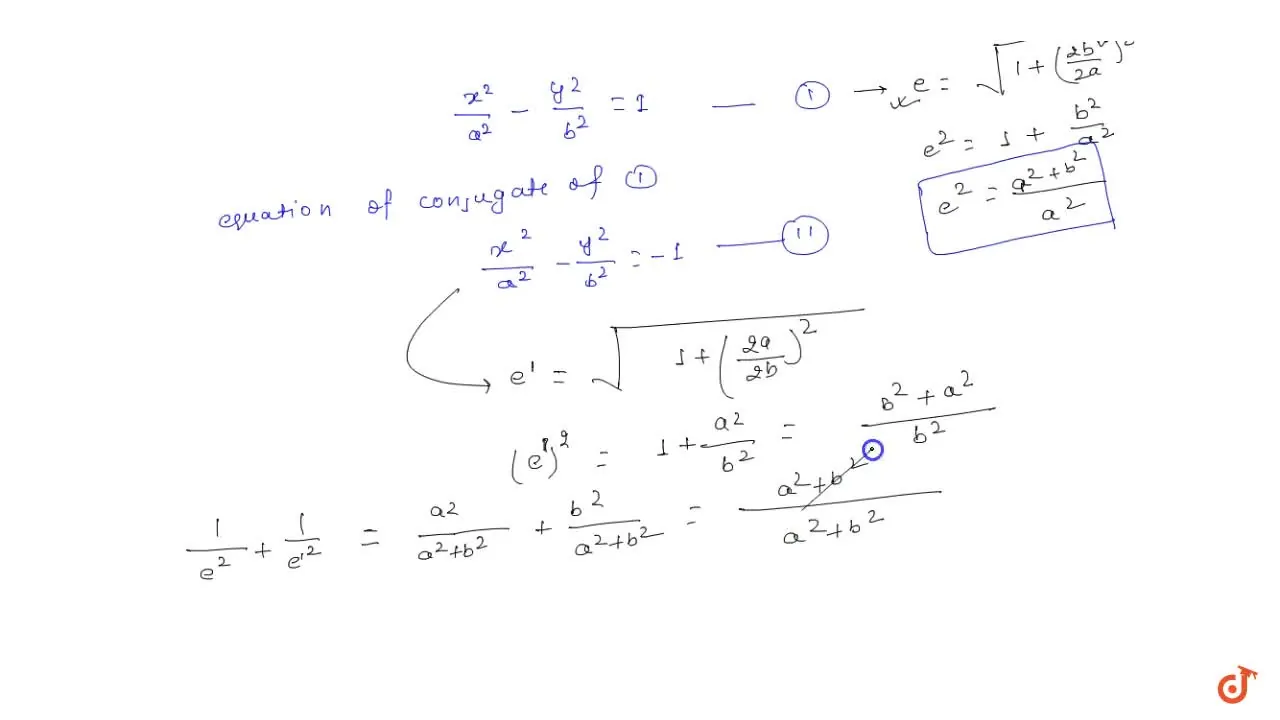
If e and e' the eccentricities of a hyperbola and its conjugate,than1e2+1e'2=.
0
1
2
none of these
The correct Answer is:B
Let x2a2−y2b2=1 be a hyperbola and let x2a2−y2b2=−1 be its conjugate. Then, their eccentricites are given by e2=a2+b2a2 and e'2=a2+b2b2 respectively.
∴1e2+1e'2=a2a2+b2+b2a2+b2=1
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Section I - Solved Mcqs53videos
HYPERBOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Section II - Assertion Reason Type4videos
HYPERBOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test30videos
FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section II - Assertion Reason Type1videos
INEQUALITIES
Similar Questions
If eande' the eccentricities of a hyperbola and its conjugate, prove that 1e2+1e'2=1.
View SolutionIf eand¯e the eccentricities of a hyperbola and its conjugate, prove that 1e2+1¯e2=1.
View SolutionIf e and e' are the eccentricities of a hyperbola and its conjugate, then 1e2+1(e')2 is equal to
View SolutionIf e1ande2 be the eccentricities of hyperbola and its conjugate, then 1e2_1+1e2_2= (A) √28 (B) 14 (C) 1 (D) 4
View SolutionIf e1ande2 are the eccentricities of a hyperbola 3x2−2y2=25 and its conjugate, then
View SolutionIf e1ande2 are the eccentricities of a hyperbola 3x2−2y2=25 and its conjugate, then
View SolutionIf a variable line has its intercepts on the coordinate axes eande′, where e2ande′□2 are the eccentricities of a hyperbola and its conjugate hyperbola, then the line always touches the circle x2+y2=r2, where r= 1 (b) 2 (c) 3 (d) cannot be decided
View SolutionIf e1 and e2 are the eccentricities of the hyperbola and its conjugate hyperbola respectively then 1e21+1e22 is equal to
View SolutionLet e1ande2 be the eccentricities of a hyperbola and its conjugate hyperbola respectively. Statement 1 : e1e2>√2. Statement 2 : 1e2_1+1e2_2=
View SolutionIf eande' are the eccentricities of the hyperbola x2a2−y2b2=1 and its conjugate hyperbola, prove that 1e2+1+e'2=1
View Solution