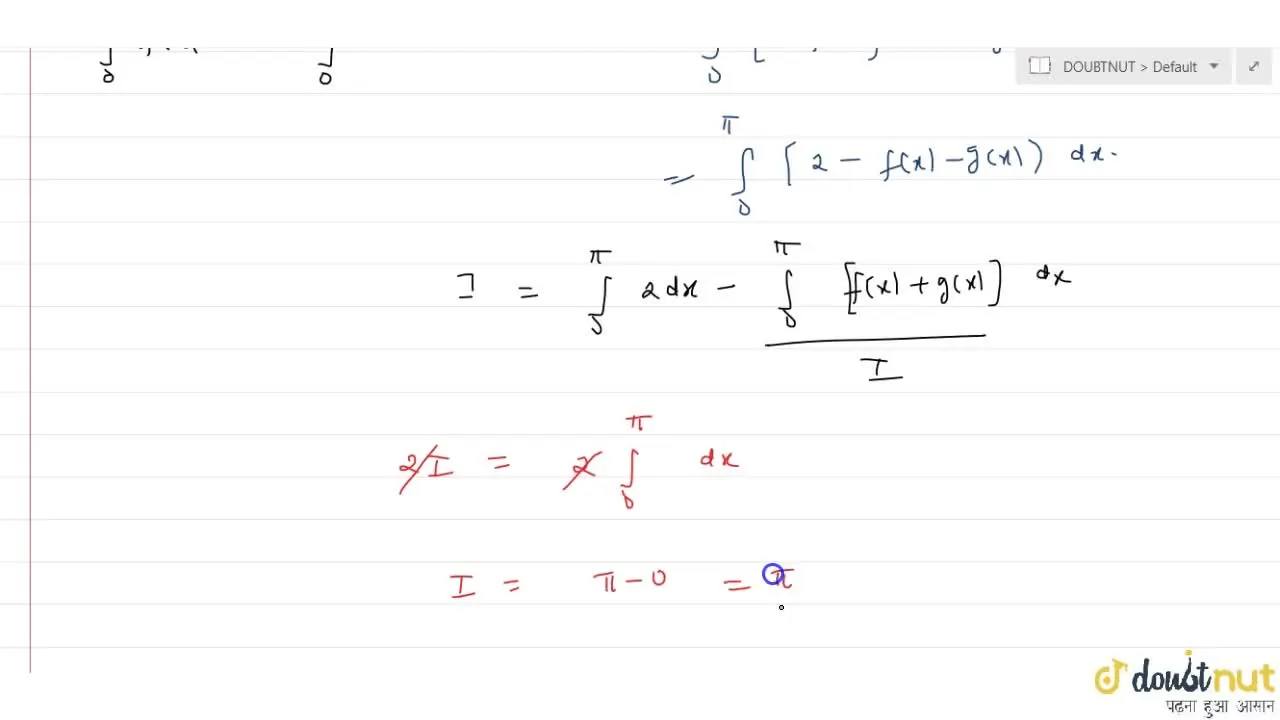If f and g are continuopus fucntions on [0,π] satisfying f(x)+f(π−x=1=g(x)+g(π−x) then ∫π0{f(x)+g(x)}dx is equal to
π
2π
π2
3π2
The correct Answer is:A
I=π∫0{f(x)+g(x)}
⇒I=π∫0{f(π−x)+g(π−x)}dx
⇒I=π∫0{1−f(x)+1−g(x)}dx[∴f(π−x)+f(x)=1andg(π−x)+G(x)=1]
⇒I=π∫02−{f(x)+g(x)]dx
⇒I=2π−I⇒2I=2π⇒I=π
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type12videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise147videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
If fandg are continuous functions on [0,π] satisfying f(x)+f(π−x)=g(x)+g(π−x)=1, then ∫π0[f(x)+g(x)] dx is equal to
View SolutionIf f(x) and g(x) are continuous functions satisfying f(x)=f(a−x) and g(x)+g(a−x)=2, then what is ∫a0f(x)g(x)dx equal to ?
View SolutionIf f(x)+f(π−x)=1 and g(x)+g(π−x)=1, then : ∫π0[f(x)+g(x)]dx=
View SolutionIf f(x) and g(x) are continuous functions satisfying f(x)=f(a−x)andg(x)+g(a−x)=2, then ∫a0f(x)g(x)dx is equal to
View SolutionIf f and g are continuous functions in [0,1] satisfying f(x)=f(a−x) and g(x)+g(a−x)=a, then ∫a0f(x).g(x)dx is equal to
View SolutionLet f and g be continuous functions on [ 0 , a] such that f(x)=f(x)=f(a−x)andg(x)+g(a−x)=4, then ∫a0f(x)g(x)dx is equal to
View SolutionLet f and g be continuous fuctions on [0, a] such that f(x)=f(a−x) and g(x)+g(a−x)=4 then ∫a0f(x)g(x)dx is equal to
View Solutionif ∫g(x)dx=g(x), then ∫g(x){f(x)+f'(x)}dx is equal to
View SolutionIf fandg are continuous function on [0,a] satisfying f(x)=f(a−x)andg(x)+g(a−x)=2, then show that ∫a0f(x)g(x)dx=∫a0f(x)dx.
View Solution∫π−πsinx[f(cosx)]dx is equal to
View Solution