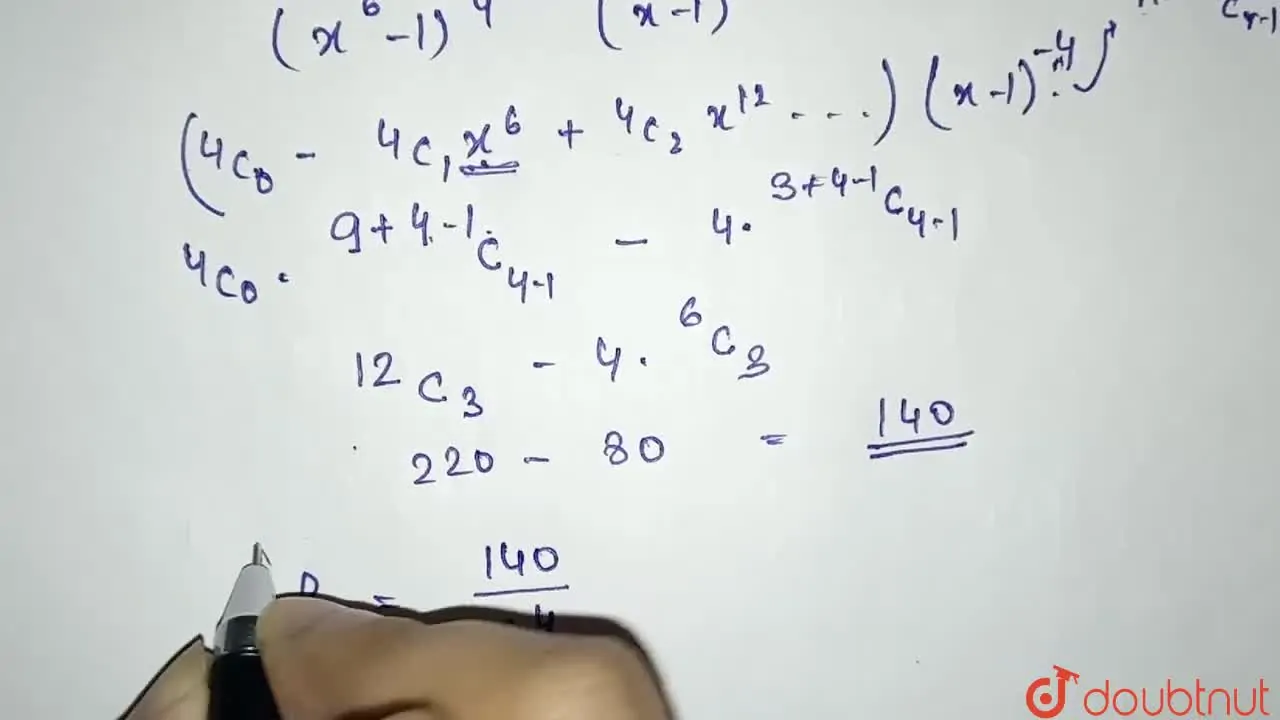If four dice are thrown together. Probability that the sum of the number appearing on them is 13, is
35324
5216
11216
11432
The correct Answer is:A
The total number of elementary events associated with the experiment of throwing four dice is 6×6×6×6=64.
Favourable number of elementary events
= Coefficient of x13 in (x1+x2+x3+x4+x5+x6)4
= Coefficient of x9 in (1+x+x2+..+x5)4
= Coefficient of x9 in (1−x61−x)4
= Coefficient of x9 in (1−x6)4(1−x)−4
=Coefficient of x9 in (1−.4C1x6+.4C2x12)(1−x)−4
= Coefficient of x9 in (1−x)−4−.4C1× Coefficient of x3 in (1−x)−4
=.9+4−1C4−1−.4C1×.3+4−1C4−1
[∵ Coeff. of xn in(1−x)−r=.n+r−1Cr−1]
=.12C3−4×.6C3=140
∴ Required probability =14064=35324
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)15videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section I - Mcqs94videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test60videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test50videos
QUADRATIC EXPRESSIONS AND EQUATIONS
Similar Questions
Three dice are thrown together. The probability that the sum of the numbers appearing on them is 9, is
View SolutionIf three six-faced fair dice are thrown together, the probability that the sum of the numbers appearing on the dice is 16 is
View SolutionThree six-faced dice are thrown together. The probability that the sum of the numbers appearing on the dice is k(3≤k≤8), is
View SolutionThree six-faced dice are thrown together. The probability that the sum of the numbers appearing on the dice is k(9≤k≤14), is
View SolutionIf two dice are thrown together . Then , the probability that the sum of the numbers appearing on them is a prime number, is
View SolutionIf three six-faced fair dice are thrown together, find the probability that the sum of the numbers appearing on the dice is 12.
View SolutionTwo dice thrown together. Then the probability that the sum of numbers appearing on them is a prime number, is
View SolutionTwo dice thrown together. Then the probability that the sum of numbers appearing on them is a prime number, is
View SolutionTwo dice are thrown. What is the probability that the sum of the numbers appearing on the two dice is 11, it 5 appears on the first?
View SolutionTwo dice are thrown. The probability that the sum of numbers appearing is more than 10, is
View Solution