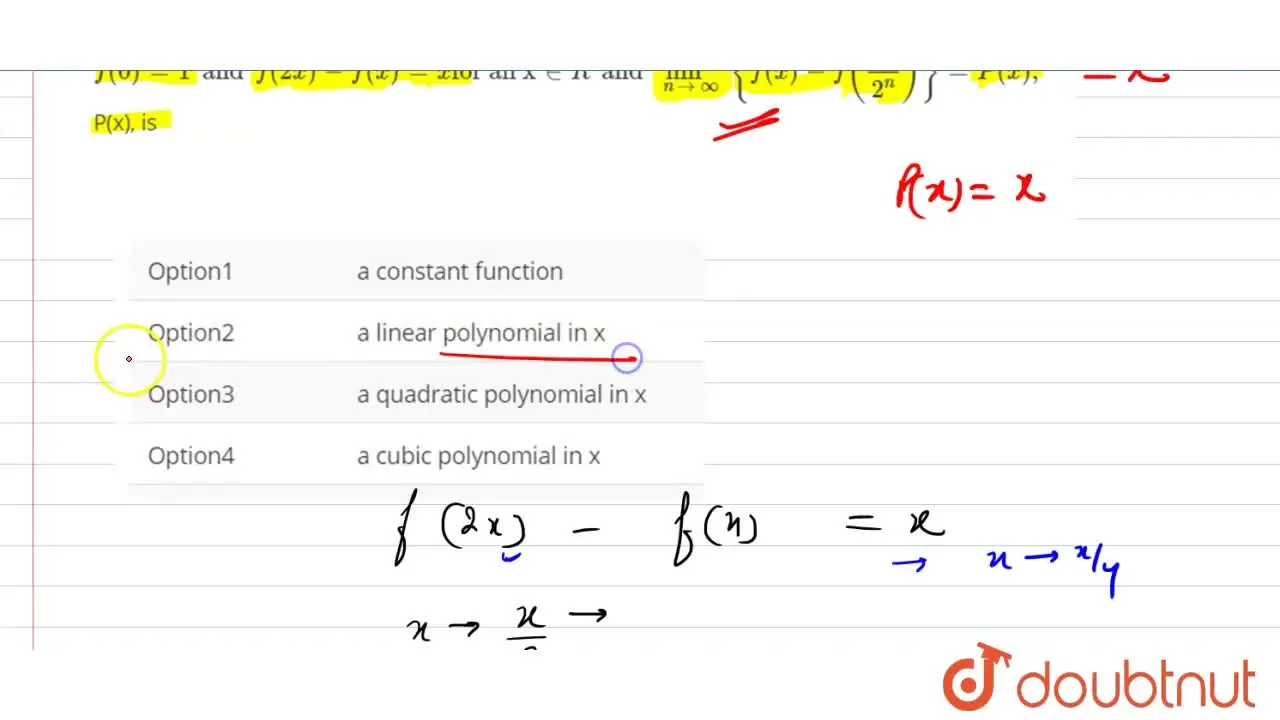
If f:R→R is a continuous function satisfying f(0)=1andf(2x)−f(x)=xfor all x∈Randlimx→∞{f(x)−f(x2n)}=P(x), P(x), is
a constant function
a linear polynomial in x
a quadratic polynomial in x
a cubic polynomial in x
The correct Answer is:B
We have f(2x)−f(x)=x
⇒f(x)−f(x2)=x2 [Replacing x byx2]
⇒f(x2)−f(x4)=x4
⇒f(x4)−f(x8)=x8
f(x2n−1)−f(x2n)=x2n
Adding up all of these questtions, we obtain
f(x)−f(x2n)=x2+x4+x8+.....+x2n
⇒f(x)−f(x2n)=x2(1−12n)(1−12)
⇒f(x)−f(x2n)=x(1−12n)
⇒limn→∞{f(x)−f(x2n)}=x
P(x)=x, which is linear polynomial in x.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
If f:R→R is a continuous function satisfying f(0)=1 and f(2x)−f(x)=x∀xεR and limn→∞(f(x)−f(x2n))=P(x). Then P(x) is
View SolutionIf f:R→R is continuous function satisfying f(0)=1 and f(2x)−f(x)=x,∀x∈R, then limn→∞(f(x)−f(x2n)) is equal to
View SolutionLet f be a continuous function satisfying f(x+y)=f(x)+f(y) for all x,y ∈ R and f(1)=5 then limx→4 f(x) is equal to
View SolutionLet f be a continuous function satisfying f(x) f(y)=f(x)+f(y)+f(xy)-2 for all x,y ∈ R and f(2)=5 then limx→4f(x) is
View Solutionf:R→R;f(x) is continuous function satisfying f(x)+f(x2)=2∀x∈R, then f(x) is
View Solutionf:R→R;f(x) is continuous function satisfying f(x)+f(x2)=2∀x∈R, then f(x) is
View SolutionIf f(x) is a continuous function satisfying f(x)f(1/x) =f(x)+f(1/x) and f(1) > 0 then limx→1 f(x) is equal to
View SolutionLet f:R→R be a continuous function such that |f(x)−f(y)|≥|x−y| for all x,y∈R , then f(x) will be
View SolutionLet f(x) be a continuous function such that f(0)=1andf(x)=f(x7)=x7∀x∈R, then f(42) is
View SolutionIf f:R→R is a differentiable function such that f(x)>2f(x) for all x∈R and f(0)=1, then
View Solution