If f:R→R is an even function having derivatives of all orders, then an odd function among the following isSolution in Telugu
f''
f'''
f'+f''
f''+f'''
The correct Answer is:B
Step by step video, text & image solution for If f:RrightarrowR is an even function having derivatives of all orders, then an odd function among the following is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-2
4 Videos
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-3
5 Videos
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - EXERCISE 1C
3 Videos
- DIFFERENTIAL EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 2
15 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - EXERCISE 2 SET -2
3 Videos
Similar Questions
1.ifF(X)=1xthenf'(1)=A2.Iff(x)=x+1x+3thenf'(−1)=B3.Iff(x)=x2thenf'(1)=C4.Iff(x)=logxthenf'(3)=D
The ascending order of A,B,C ,D is
View SolutionMatch the following
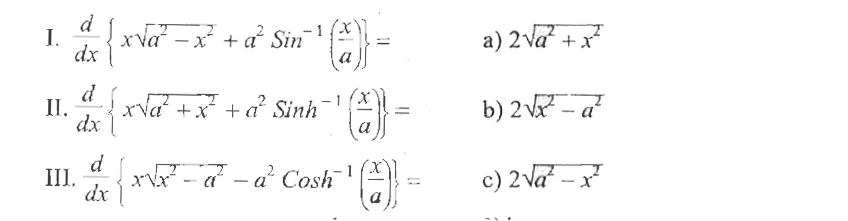
View SolutionThe function y=Sin−1(cosx) is not differentiable at
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
View SolutionThe derivative of an even function is always an odd function.
View SolutionProve that the derivative of (a) an odd function is an even function;
View SolutionProve that the derivative of an even function is an odd function and that of an odd function is an even function.
View Solutionएक विषम फलन का अवकलज सदैव एक सम फलन होता है-
View SolutionProve that the derivative of and odd function is an even function.
View SolutionIf f:R→R is an even function having derivatives of all orders, then an odd function among the following is
View SolutionFunctions|Even and Odd functions
View SolutionThe derivative of an even function is always an odd function.
View SolutionProve that the derivative of an even function is an odd function and that of an odd function is an even function.
View SolutionProve that the product of two even or two odd functions is an even function, whereas the product of an even and an odd function is an odd function.
View Solution
