If f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(f⋅g)(x)
To find the expression for the function (f⋅g)(x), where f(x)=3x−2 and g(x)=x2−4, we will follow these steps:
Step 1: Write the expression for (f⋅g)(x)
We know that (f⋅g)(x)=f(x)⋅g(x). Therefore, we can write:
(f⋅g)(x)=(3x−2)⋅(x2−4)
Step 2: Distribute the terms
Now, we will distribute 3x and −2 across the terms in g(x):
(f⋅g)(x)=3x⋅(x2−4)−2⋅(x2−4)
Step 3: Calculate each product
Calculating the first product:
3x⋅(x2−4)=3x3−12x
Calculating the second product:
−2⋅(x2−4)=−2x2+8
Step 4: Combine the results
Now, we combine the results from the two products:
(f⋅g)(x)=(3x3−12x)+(−2x2+8)
Step 5: Rearrange the expression
Rearranging the terms gives us:
(f⋅g)(x)=3x3−2x2−12x+8
Final Expression
Thus, the expression for (f⋅g)(x) is:
(f⋅g)(x)=3x3−2x2−12x+8
---
We know that (f⋅g)(x)=f(x)⋅g(x). Therefore, we can write:
(f⋅g)(x)=(3x−2)⋅(x2−4)
Now, we will distribute 3x and −2 across the terms in g(x):
(f⋅g)(x)=3x⋅(x2−4)−2⋅(x2−4)
Calculating the first product:
3x⋅(x2−4)=3x3−12x
Calculating the second product:
−2⋅(x2−4)=−2x2+8
Now, we combine the results from the two products:
(f⋅g)(x)=(3x3−12x)+(−2x2+8)
Rearranging the terms gives us:
(f⋅g)(x)=3x3−2x2−12x+8
Thus, the expression for (f⋅g)(x) is:
(f⋅g)(x)=3x3−2x2−12x+8
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution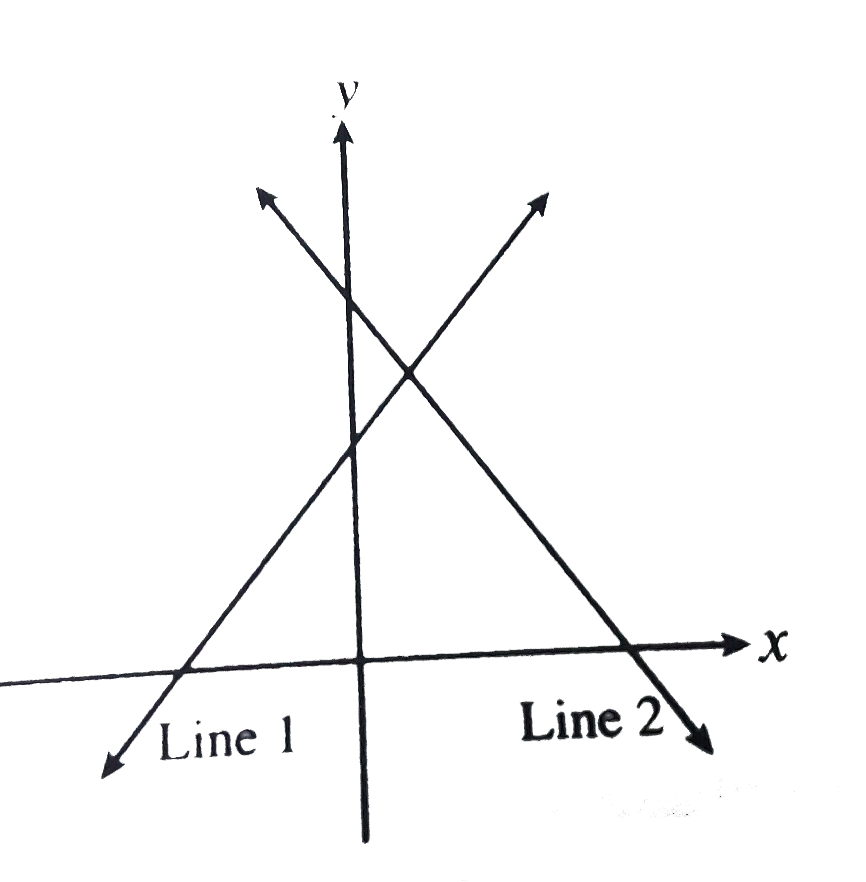
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View SolutionIf the functions of f and g are defined by f(x)=3x-4 and g(x)=2+3x then g^(-1)(f^(-1)(5))
View SolutionIf f(x) and g(x) are continuous functions, then ∫In(1/λ)Inλf(x2/4)[f(x)−f(−x)]g(x2/4)[g(x)+g(−x)]dx is
View SolutionLet f(x) = 3x + 8 and g(x)=x2 be two real functions. Find (f+g) (x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(f+g)(x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(f-g)(x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(fg)(x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(f∘g)(x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(g∘f)(x)
View SolutionIf g(x)=3x+2andg(f(x))=x, then f(2)=
View SolutionLet f(x)=x3+3x+2 and g(x) is inverse function of f(x) then the value of g'(6) is
View SolutionIf f(x) = 3x -11, and g(x) =x2−1, find each fo the following :
(f+g)(x)
View SolutionIf f(x) = 3x -11, and g(x) =x2−1, find each fo the following :
(g−f)(2)
View Solution
