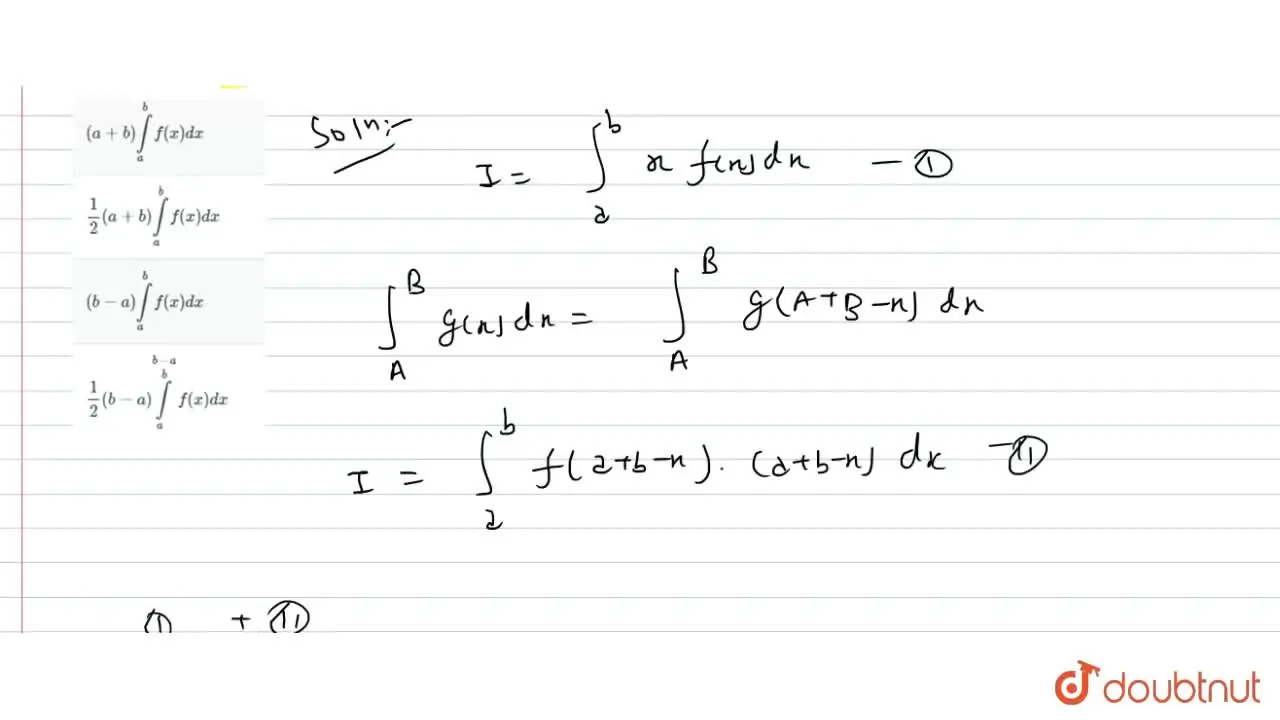
If f(x)=f(a+b-x), then ∫baxf(x)dx is equal to
A
(a+b)b∫af(x)dx
B
12(a+b)b∫af(x)dx
C
(b−a)b∫af(x)dx
D
12(b−a)b−ab∫af(x)dx
Video Solution
Text Solution
The correct Answer is:B
Let I=b∫axf(x)dx. Then,
I=b∫a(a+b−x)f(a+b−x)dx
⇒I=(a+b)b∫af(a+b−x)dx−b∫axf((a+b−x)dx
⇒I=(a+b)b∫af(x)dx−b∫axf(x)dx[∵f(a+b−x)=f(x)]
⇒I=(a+b)b∫af(x)dx−I
⇒2I=(a+b)b∫af(x)dx⇒I=a+b2b∫af(x)dx
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section I - Solved Mcqs145videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type12videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
∫b+ca+cf(x)dx is equal to:
View SolutionIf (2a+2b−x)=f(x), then ∫2b2ax f(x) dx is equal to
View SolutionIf f(a+b−x)=f(x), then ∫baxf(x)dx is equal to
View SolutionIf f(3−x)=f(x), then ∫21xf(x)dx is equal to
View SolutionIf f(a+b−x)=f(x), then ∫baxf(x)dx=
View SolutionIf f(a+b−x)=f(x), then ∫baxf(x)dx is equal to
View SolutionIf f(a+b−x)=f(x), then ∫baxf(x)dx is equal to (A) a−b2∫baf(a+b−x)dx (B) a+b2∫baf(b−x)dx (C) a+b2∫baf(x)dx (D) b−a2∫baf(x)dx
View SolutionIf f(a+b−x)=f(x), then ∫baxf(x)dx is equal to a+b2∫baf(b−x)dx b. a+b2∫baf(b+x)dx c. b−12∫baf(x)dx d. a+b2∫baf(x)dx
View SolutionIf f(x)=f(2−x) then ∫1.50.5xf(x)dx=
View Solution∫baf(x)dx=
View Solution