If l = 2, m = 4
Column - IColumn - II(A) 1m(p) 2(B) m1(q) 16(C) 1m(r) 12(D) 12m(s) 8(t) 32(u) 1
To solve the problem, we will evaluate each expression in Column I using the given values of l=2 and m=4 and then match them with the corresponding values in Column II.
1. Evaluate lm:
- Substitute the values:
lm=24
- Simplify:
24=12
- Match with Column II: 12 corresponds to (r).
2. Evaluate ml:
- Substitute the values:
ml=42
- Simplify:
42=2
- Match with Column II: 2 corresponds to (p).
3. Evaluate l×m:
- Substitute the values:
l×m=2×4
- Calculate:
2×4=8
- Match with Column II: 8 corresponds to (s).
4. Evaluate l2×m:
- Substitute the values:
l2×m=22×4
- Calculate 22:
22=4
- Now multiply:
4×4=16
- Match with Column II: 16 corresponds to (q).
Final Matches:
- (A) lm matches with (r) 12
- (B) ml matches with (p) 2
- (C) l×m matches with (s) 8
- (D) l2×m matches with (q) 16
- Substitute the values:
lm=24
- Simplify:
24=12
- Match with Column II: 12 corresponds to (r).
- Substitute the values:
ml=42
- Simplify:
42=2
- Match with Column II: 2 corresponds to (p).
- Substitute the values:
l×m=2×4
- Calculate:
2×4=8
- Match with Column II: 8 corresponds to (s).
- Substitute the values:
l2×m=22×4
- Calculate 22:
22=4
- Now multiply:
4×4=16
- Match with Column II: 16 corresponds to (q).
- (A) lm matches with (r) 12
- (B) ml matches with (p) 2
- (C) l×m matches with (s) 8
- (D) l2×m matches with (q) 16
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the corresponding entries of column 1 with column 2. [Where m is the magnification produced by the mirror.
Column 1Column 2(A)m=−2(a) Convex mirror(B)m=−12(b) Concave(C)m=+2(c) Real image(D)m=+12(d) Virtual imageAA→aandc,B→aandd,C→aandb,D→canddBA→aandd,B→bandc,C→bandd,D→bandcCA→candd,B→bandd,C→bandc,D→aanddDA→bandc,B→bandc,C→bandd,D→aandd
A semicircular ring has mass m and radius R as shown in figure. Let I1,I2,I3andI4 be the moments of inertia of the four axes as shown. Axis 1 passes through centre and is perpendicular to plane of ring. Then, match the following columns.
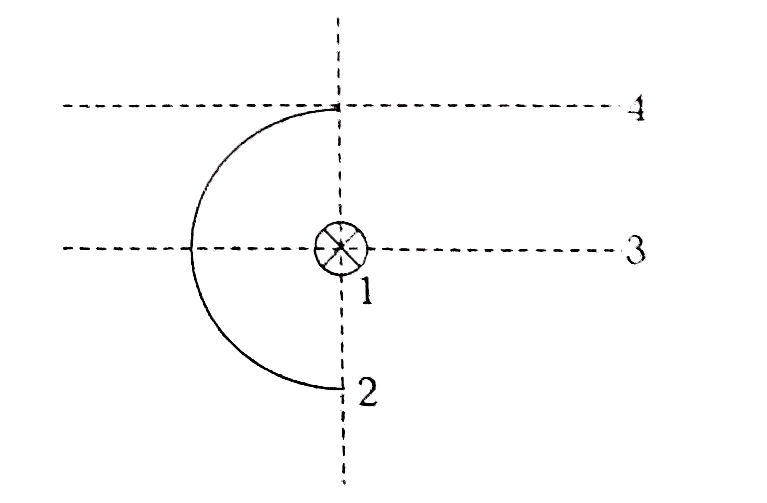
Column-IColumn-II(A)I1(p)mR22(B)I2(q)(3/2)mR2(C)I3(r)mR2(D)I4(s)Data is insufficientView SolutionFour rods of equal length l and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say I1,I2andI3. Then, match the following columns

Column-IColumn-II(A)I1(p)43ml2(B)I2(q)23ml2(C)I3(r)12ml2(s)NoneView SolutionColumnIColumnII(A)1s(p)ml=0(B)2pz(q)Nodal planes=2(C)3dxy(r)Radial nodes=0(D)3dz2(s)Number of maxima=1
View SolutionColumn IColumn II(A)Work(p)[A1/2T−1](B)Moment of inertia(q)[FA1/2](C)Velocity(r)[FA1/2T2]
View SolutionMatch Column - I with Column - II
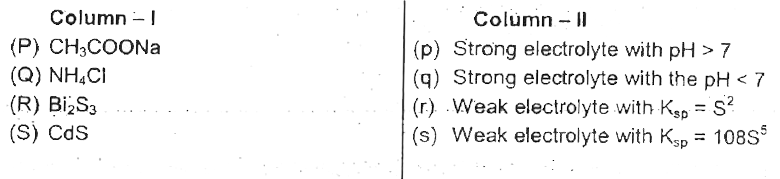
PQRS(A)1243(B)2143(C)4132(D)4321View Solution[D] Match the solutions in Column-I in Column-I with their osmotic properties in Column-II :
Column-IColumn-II(a)S1:0.1M glucose,S20.1M urea(p)S1andS2 are isotonic(b)S1:0.1M NaCl, S2:0.1MNa2SO4(q)No migration of solvent across the membrane(c)S1:0.1 NaCl, S2=0.1MKCl(r)S1 is hypertonic to S2(d)S1:0.1MCuSO4, S2:0.1M sucorse(s)S1 is hypotonic to S2
[Note : Assume that the electrolytes are completely ionised.View SolutionColumn IColumn II(A)1fermi(p)10−13m(B)1X-ray unit(q)10−15m(C)1angstrom(r)10−10m(D)1Astronomical unit(s)9.46×1015m(E)1Light year(t)3.26Light year(F)1Parse(u)3.08×1016m(v)1.49×1011m
View Solution

