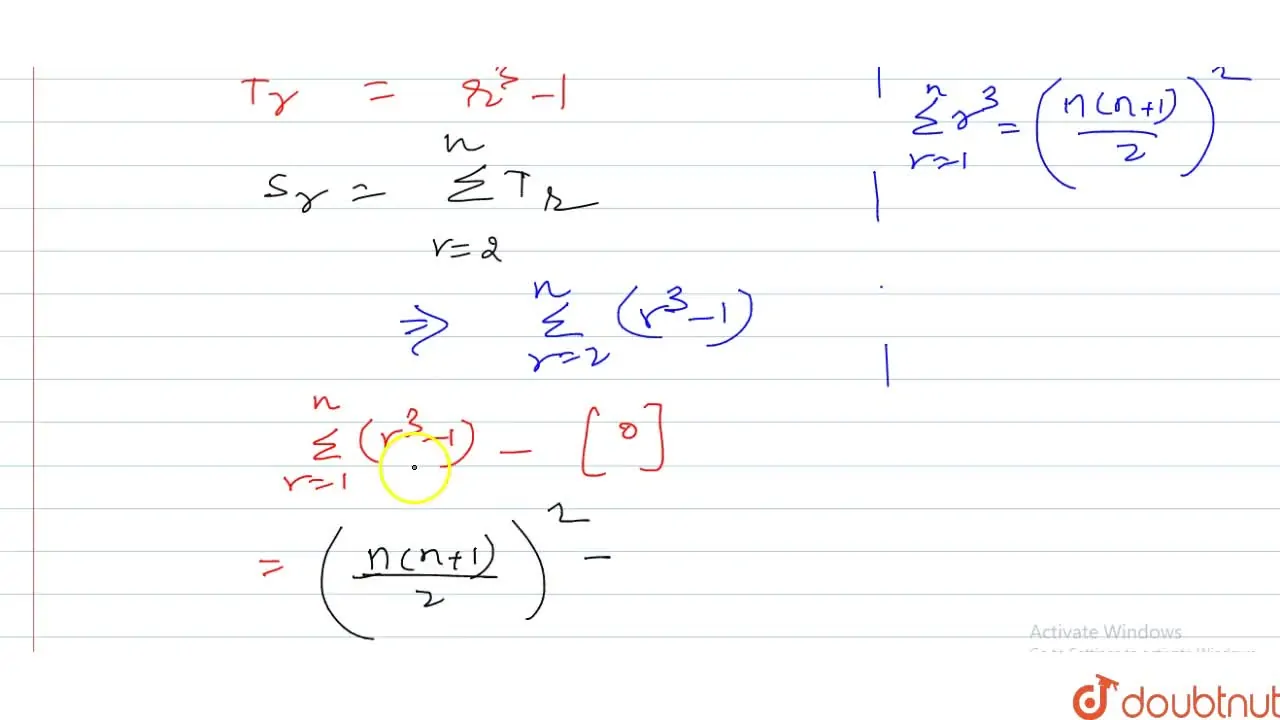The value of the expression 1.(2−ω).(2−ω2)+2.(3−ω)(3−ω2)+.+(n−1)(n−ω)(n−ω2), where omega is an imaginary cube root of unity, is………
{n(n+1)2}2
{n(n+1)2}2−n
{n(n+1)2}2+n
none of these
The correct Answer is:B
We have,
(z−1)(z−ω)(z−ω2)=z3−1
∴1(2−ω)(2−ω2)+2(3−ω)(3−ω2)+….++(n−1)(n−ω)(n−ω2)
=n∑r=2(r−1)(r−ω)(r−ω2)
=n∑r=2(r3−1)=n∑r=2r3−n∑r=21=(n∑r=2r3)−1−(n∑r=21)
={n(n+1)2}2−1−(n−1)={n(n+1)2}2−n
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section I - Solved Mcqs141videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type15videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
The value of the expression
1⋅(2−ω)(2−ω2)+2⋅(3−ω)(3−ω2)+....+(n−1)⋅(n−ω)(n−ω2),where ω is an imaginary cube root of unity isView SolutionThe value of the expression , (2−w)(2−w2)+2.(3−w)(3−w2)+.............+(n−1).(n−w)(n−w2), where w is an imaginary cube root of unity is
View SolutionThe value of the expression (1+1ω)(1+1ω2)+(2+1ω)(2+1ω2)+(3+1ω)(3+1ω2)+…………..+(n+1ω)(n+1ω2), where ω is an imaginary cube root of unity, is
View SolutionIf ω is a complex cube root of unity, then the value of the expression 1(2−ω)(2−ω2)+2(3−ω)(3−ω2)+...+(n−1)(n−ω)(n−ω2)(n≥2) is equal to (A) n2(n+1)24−n (B) n2(n+1)24+n (C) n2(n+1)4−n (D) n(n+1)24−n
View SolutionEvaluate: ∣∣ ∣ ∣∣1111ω2ω1ωω2∣∣ ∣ ∣∣ (where ω is an imaginary cube root unity).
View SolutionThe value of the expression (1+1ω)(1+1ω2)+(2+1ω)(2+1ω2)+(3+1ω2)+…………..+(n+1ω)(n+1ω2), where ω is an imaginary cube root of unity, is
View SolutionThe value of the expression 2(1+1ω)(1+1ω2)+3(2+1ω)(2+1ω2)+4(3+1ω)(3+1ω2)+.......+(n+1)(n+1ω)(n+1ω2) where ω is an imaginary cube roots of unity, is:
View SolutionThe value ∣∣ ∣ ∣∣1+ωω2−ω1+ω2ω−ω2ω2+ωω−ω2∣∣ ∣ ∣∣ is equal to ( ω is an imaginary cube root of unity)
View SolutionThe area of a quadrilateral whose vertices are 1,i,ω,ω2, where (ω≠1) is a imaginary cube root of unity, is
View SolutionEvaluate ∣∣ ∣ ∣∣1ωω2ωω21ω2ωω∣∣ ∣ ∣∣ where ω is cube root of unity.
View Solution