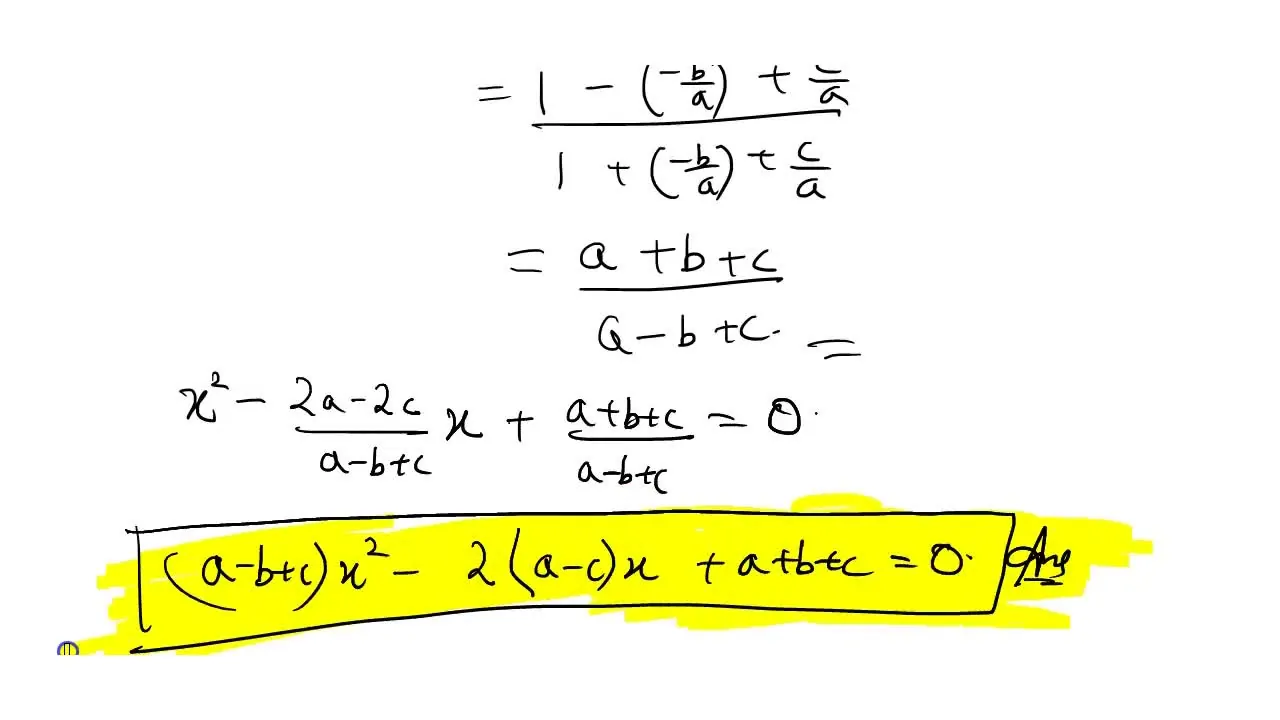If roots of the equation ax2+bx+c=0 are αandβ , find the equation whose roots are 1α,1β (ii) α,−β (iii) 1−α1+α,1−β1+β
Here in all cases, functions of αandβ are symmetric.
(i) Let 1α=yorα=1y
Now α is a root of the equation ax2+bx+c=0 . Thus,
aα2+bα+c=0
or ay2+by+c=0
or cy2+by+a=0
Hence, the requried equation is cx2+bx+a=0
We get same equation if we start with 1β=y
(ii) Let −α=yorα=−y
Now α is root of the equation ax2+bx+c=0. Thus ,
aα2+bα+c=0
Hence, the required is ax2−bx+c=0
(iii) Let 1−α1+α=yorα=1−y1+y
Now α is root of the equation ax2+bx+c=0.Thus ,
aα2+bα+c=0
or a(1−y1+y)2+b(1−y1+y)+c=0
Hence, required equation is
a(1−x)2+b(1−x2)+c(1+x)2=0
Related Playlists
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.13videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.25videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension12videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If roots of the equation ax2+bx+c=0 are αandβ , find the equation whose roots are 1α,1β (ii) −α,−β (iii) 1−α1+α,1−β1+β
View SolutionIf the equation x2+2x+5=0 has two roots αandβ then the equation whose roots are α+1αandβ+1β is
View SolutionIf α,β are the roots of the equation 3x2+2x+1=0 , then find the equation whose roots are 1−α1+α,1−β1+β
View SolutionIf α and β are the roots of the equation x2+x+1=0, the equation whose roots are α19 and β7 is
View SolutionLet αandβ are the roots of the equation x2+x+1=0 Then. The equation whose roots are α19,β7 is :
View SolutionIf α,β are the roots of the equation x2−px+q=0 and α1,β1 be the roots of the equation x2−qx+p=0, then form the quadratic equation whose roots are 1α1β+1αβ1 and 1α1α+1ββ1
View SolutionIf α,β are roots of the equation x2+x+1=0, then the equation whose roots are αβandβα, is
View SolutionIf α,β are roots of the equation x2+lx+m=0 , write an equation whose roots are −1α and−1β.
View SolutionIf α,β are the roots of ax2+bx+c=0 then find the equation whose roots are 1α2,1β2
View SolutionIf α and β are the roots of the equation ax2+bx+c=0, then find the equation whose roots are given by (i)α+1β,β+1α
View Solution