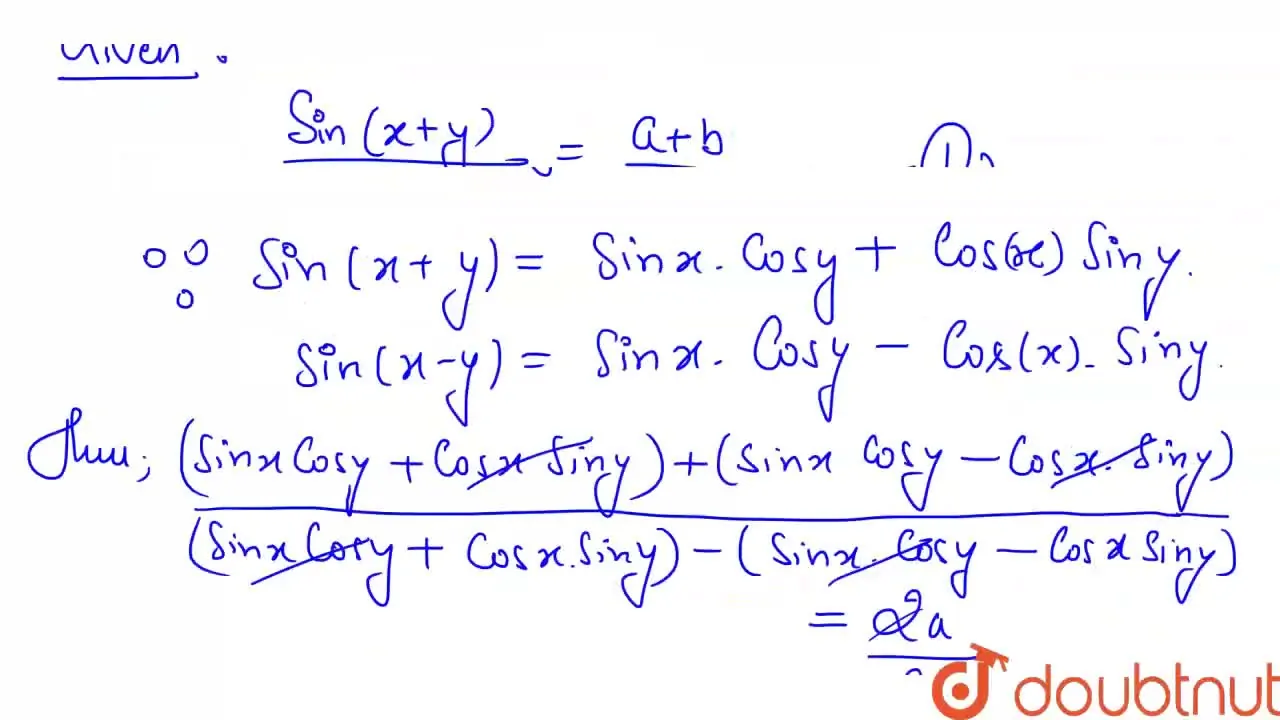If sin(x+y)sin(x−y)=a+ba−b , then show that tanxtany=ab.
A
ba
B
ab
C
ab
D
1
Video Solution
Text Solution
The correct Answer is:B
sin(x+y)sin(x−y)=a+ba−b
Applying componendo and dividendo , we get
sin(x+y)+sin(x−y)sin(x+y)−sin(x−y)=(a+b)+(a−b)(a+b)−(a−b)
⇒2sin.cosy2cos.siny=2a2b⇒tanx.coty=ab
∴tanxtany=ab
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If sin(x+y)sin(x−y)=a+ba−b , show that tanxtany=ab .
View SolutionIf sin(x+y)sin(x−y)=a+ba−b, then what is tanxtany equal to?
View Solutionsin(x+y)sin(x−y)=a+ba−b, then tanxtany=?
View SolutionIf sin(x+y)sin(x−y)=a+ba−b, then tanxtany is equal to
View SolutionIf sin(x+y)sin(x−y)=a+ba−b, then tanxtany is equal to
View Solutionsin(x−y)sin(x+y)=35then tanx. coty is
View SolutionIf sin(x−y)sin(x+y)=35, then tanx⋅coty is _____
View SolutionFind dydx when (tanx)y=(tany)x
View SolutionIf y=sin(x+a)sin(x+b),a≠b, then y is
View SolutionIf tanx=ab then show that asinx−bcosxasinx+bcosx=a2−b2a2+b2
View Solution