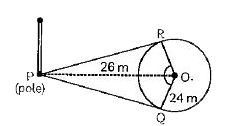
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2 m

Updated on:21/07/2023

Answer

Step by step video, text & image solution for If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-I) TYPE QUESTIONS
30 Videos
SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos

Knowledge Check

Distance between two consecutive crests is
A $λ$
B $λ / 2$
C $\frac{λ}{4}$
D $2 λ$
The distance between two consecutive antinodes is
A $\frac{λ}{4}$
B $\frac{λ}{2}$
C $λ$
D $2 λ$
The distance between two consecutive antinodes is,
A $2 λ,$
B $\frac{λ}{4}$
C $\frac{λ}{2}$
D $λ$