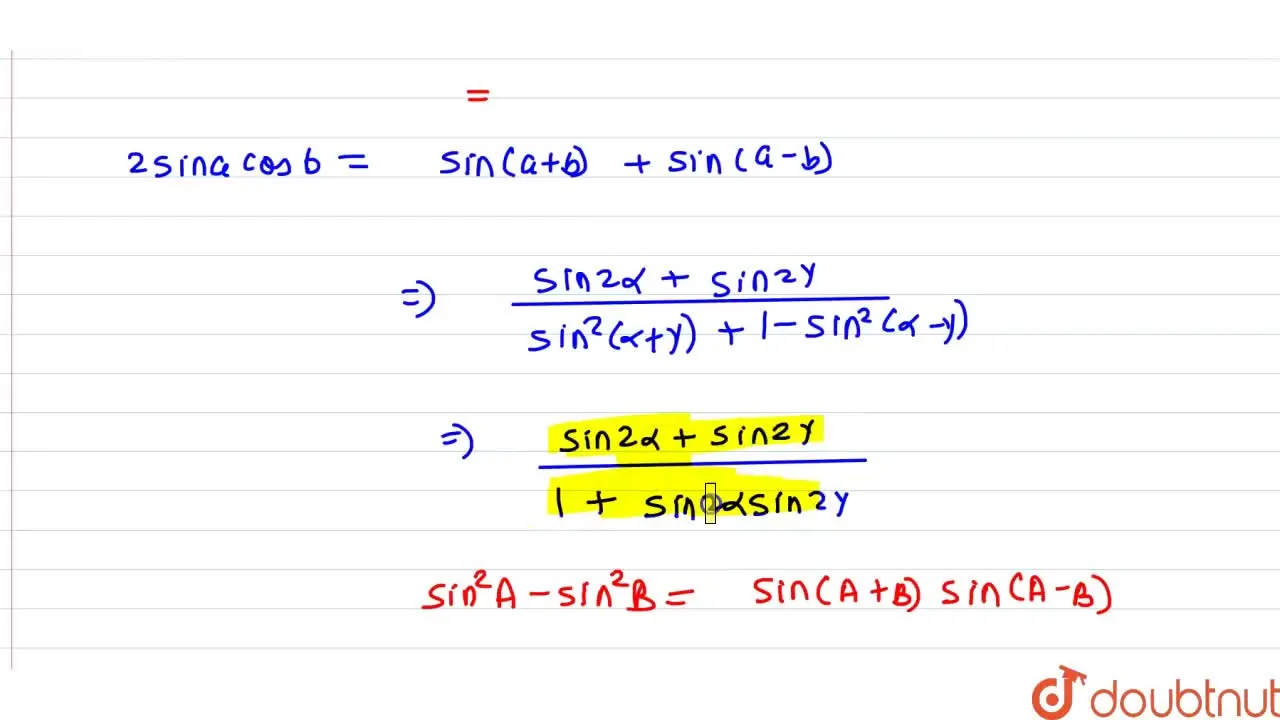If tanβ=tanα+tanγ1+tanαtanγ. prove that sin2β=sin2α+sin2γ1+sin2αsin2γ .
Video Solution
Text Solution
tanβ=tanα+tanγ1+tanαtanγ
⇒tanβ=sinαcosα+sinγcosγ1+sinαcosα⋅sinγcosγ
=sinαcosγ+sinγcosαcosαcosγ+sinαsinγ
⇒tanβ=sin(α+γ)cos(α−γ)
Now, sin2β=2tanβ1+tan2β
=2sin(α+γ)cos(α−γ)1+sin2(α+γ)cos2(α−γ)
=2sin(α+γ)cos(α−γ)cos2(α−γ)+sin2(α+γ)
=sin(α+γ+α−γ)+sin(α+γ−α+γ)(1+cos2(α−γ)2)+(1−cos2(α+γ)2)
=sin2α+sin2γ1+12(cos(α−γ)−cos(α+γ))
=sin2α+sin2γ1+12(2sin2αsin2γ)
=sin2α+sin2γ1+sin2αsin2γ=R.H.S.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If tanβ=tanα+tanγ1+tanαtanγ. prove that sin2β=sin2α+sin2γ1+sin2αsin2γ .
View SolutionIf tanβ=tanα+tanγ1+tanα.tanγ
Prove that sin2β=sin2α+sin2γ1+sin2α.Sin2γView SolutionIf tanβ=tanα+tanγ1+tanαtanγand2β=sin2α+sin2γλ+sin2αsin2γ then find the value of λ,
View SolutionIf α+β+γ=π, prove that sin2α+sinβ−sin2γ = 2sinαsinβcosγ
View SolutionIf α,β,γ,∈(0,π2) , then prove that si(α+β+γ)sinα+sinβ+sinγ<1
View SolutionGiven α+β−γ=π, prove that sin2α+sin2β−sin2γ=2sinαsinβcosγ.
View SolutionGiven α+β−γ=π,prove that sin2α+sin2β−sin2γ=2sinαsinβcosγ
View SolutionIf tan(α+β−γ)tan(α−β+γ)=tanγtanβ,(β≠γ) then sin2α+sin2β+sin2γ= (a)0 (b)1 (c) 2(d)12
View SolutionIf α+β−γ=π, prove that sin2α+sin2β−sin2γ=2sinαsinβcosγ.
View SolutionIf tanβ=2sinαsinγcosec(α+γ), then cotα,cotβ,cotγ are in
View Solution