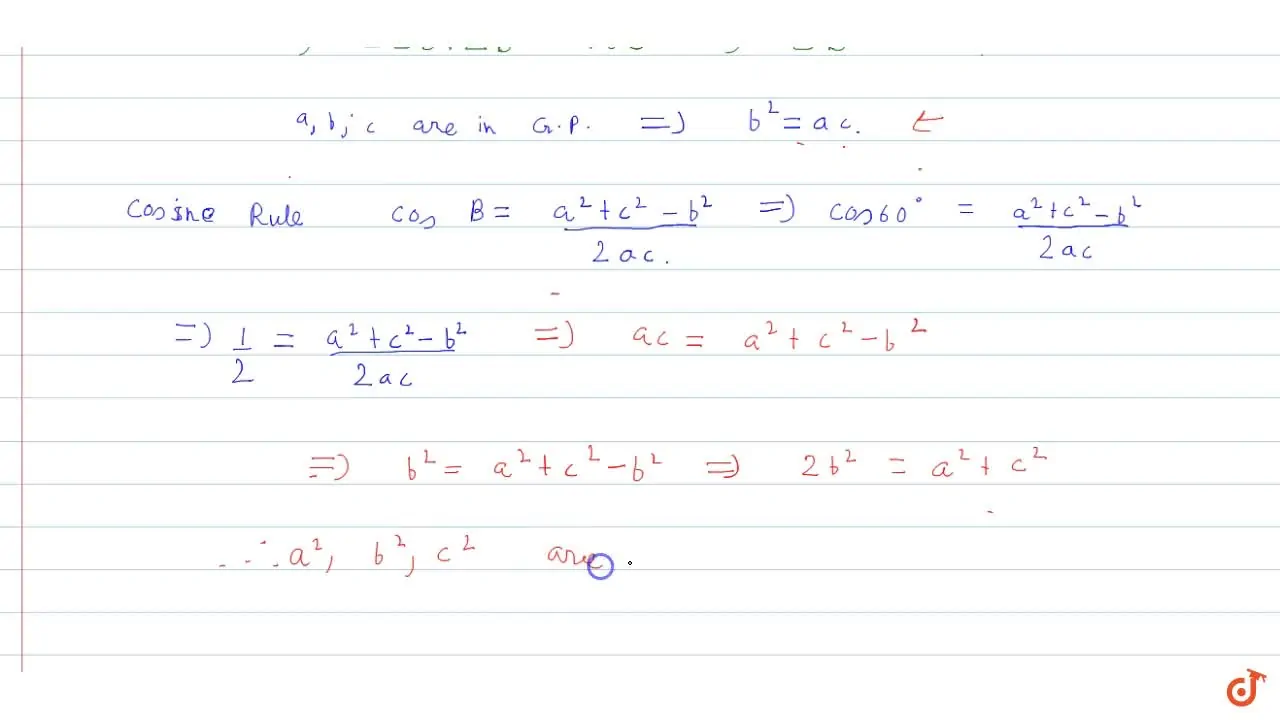If the angles A,B,C of a triangle are in A.P. and sides a,b,c, are in G.P., then prove that a2,b2,c2 are in A.P.
As angles A,BandC are in A.P.
∴2B=A+C
Now, A+B+C=180⇒B+2B+180
⇒3B=180⇒B=60∘
Now, cosB=a2+c2−b22ac
⇒cos60∘=a2+c2−b22ac
⇒12=a2+c2−b22ac
⇒ac=a2+c2−b2→(1)
Also, it is given that, a,bandc are in G.P.
∴b2=ac
Using, b2=ac in(1),
⇒b2=a2+c2−b2
⇒2b2=a2+c2
Hence, a2,b2andc2 are in A.P.
Related Playlists
Similar Questions
If the angles A,B,C of a triangle are in A.P. and sides a,b,c, are in G.P., then prove that a2,b2,c2 are in A.P.
View SolutionIf the angles A,B,C of a triangle are in A.P.and sides a,b,c are in G.P. ,then a2,b2,c2 are in
View SolutionIf the angles A,B,C of △ABC are in A.P., and its sides a, b, c are in Gp., show that a2,b2,c2 are in A.P.
View SolutionIf the angles A,B,C of ΔABC are in A.P. And its sides a,b,c are in G.P., then a2,b2,c2 are in
View SolutionIf a,b,c are in G.P., then prove that logan,logbn,logcn are in A.P.
View SolutionIf in ΔABC, sides a, b, c are in A.P. then
View SolutionIf the anngle A,B,C of a ΔABC are in A.P then :-
View SolutionIf a,b,c are in G.P. then prove that 1a+b,12b,1b+c are also in A.P.
View SolutionIf a,b,c are in A.P. as well as in G.P. then
View SolutionIf the angle A, B, C of a triangle are in A.P. such that sin(2A+B)=1/2 then sin(B+2C)=
View Solution