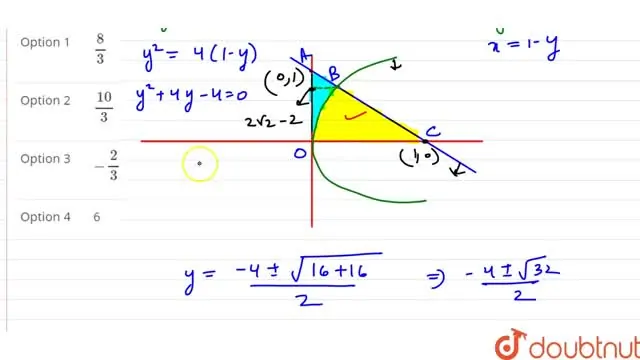
If the area (in sq. units) of the region {(x,y):y2≤4x,x+y≤1,x≥0,y≥0} is a√2+b, then a−b is equal to :
A
103
B
6
C
83
D
−23
Video Solution
Text Solution
The correct Answer is:B
Given region is (x,y):y2≤4x,x+y≤1,x≥0,y≥0}

Now, for point P, put value of y=1−x to y2=4x, we get
(1−x)2=4x⇒x2+1−2x=4x
⇒x2−6x+1=0
⇒x=6±√36−42
=3±2√2.
Since., x-coordinate of P less than x-coordinate of point A(1, 0).
∴x=3−2√2
Now, required area
=∫3−2√202√2dx+∫13−2√2(1−x)dx
=2∣∣∣x3/23/2∣∣∣3−2√20+[x−x22]13−2√2
=43(3−2√2)3/2+(1−12)−(3−2√2)+(3−2√2)22
=43[(√2−1)2]3/2+12−3+2√2+12(9+8−12√2)
=43(√2−1)3−52+2√2+172−6√2
=43(2√2−3(2)+3(√2)−1)−4√2+6
=43(5√2−7)−4√2+6=8√23−103
=a√2+b (given)
So, on comparing a=83andb=−103
∴a−b=83+103=6
|
Updated on:21/07/2023
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION55videos
AREA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)8videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )8videos
BINOMIAL THEOREM
Similar Questions
The area (in sq. units)of the region A={(x,y):x2≤y≤x+2} is :
View SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View SolutionThe area (in sq. units) of the region A={(x,y):x2≤y≤x+2} is :
View SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},isView SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} isView SolutionThe area (in sdq. Units) of the region {(x,y):y2≥2x and x2+y2≤4x,x≥0,y≥0} is
View SolutionThe area (in square units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View Solutionx−y≤2,x+y≤4,x≥0,y≥
View SolutionThe area (in sq. units) of the region {(x,y)∈R2:x2≤y≤3−2x}, is :
View Solution