If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
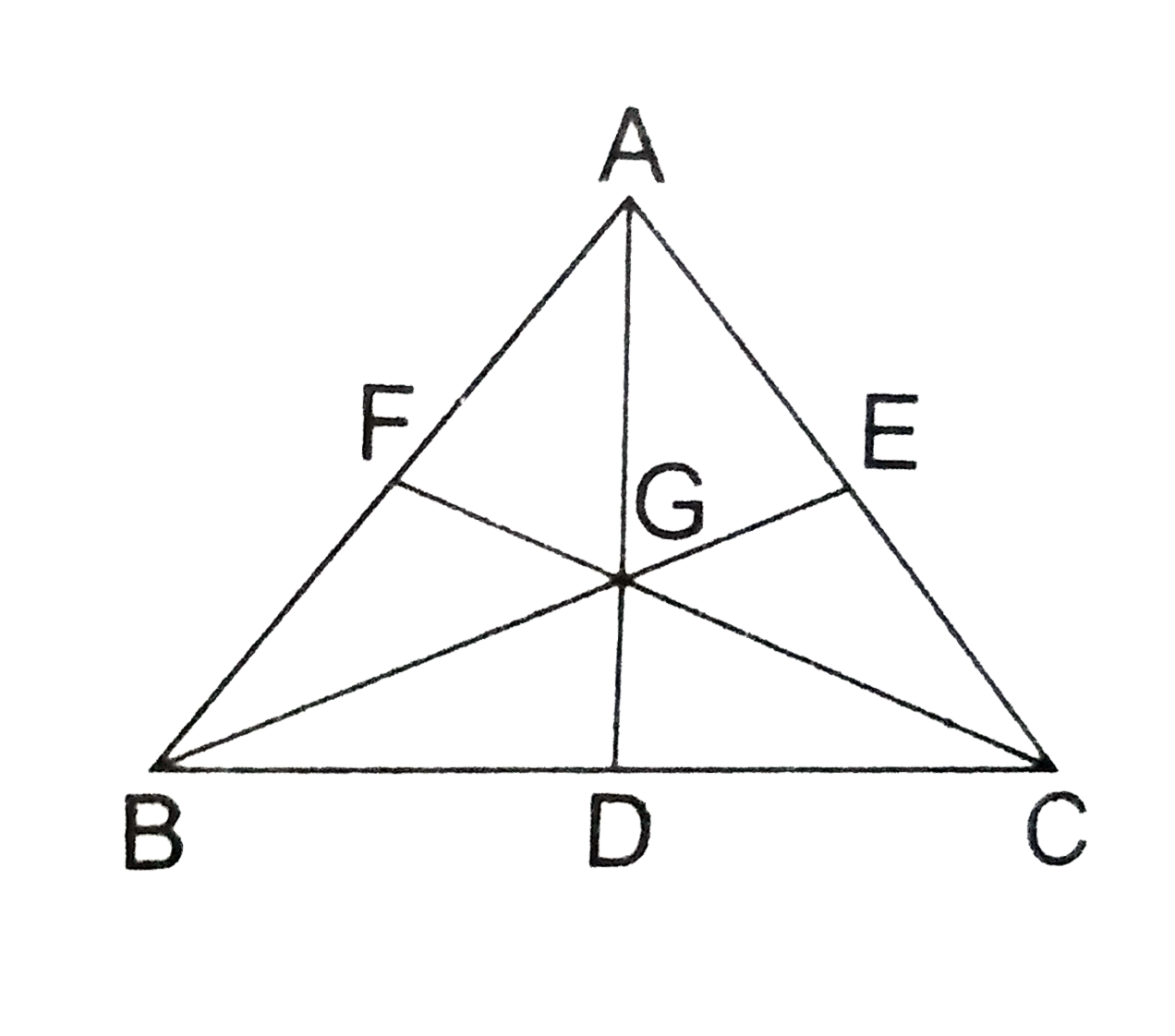
Given In ΔABC,AD,BE and CF are medians and intersect at G.
To prove ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
Proof We know that, a median of a triangle divides it into two triangles of equal area.
In ΔABC,AD is a median.
∴ ar(ΔABD)=ar(ΔACD) ...(i)
In ΔBGC,GD is a median.
∴ ar(ΔGBD)=ar(ΔGCD) ...(ii)
On substracting Eq. (ii) from Eq. (i), we get
ar(ΔABD)−ar(ΔGBD)=ar(ΔACD)−ar(ΔGCD)
⇒ ar(ΔAGB)=ar(ΔAGC) ...(iii)
Similarly,
ar(ΔAGB)=ar(ΔBGC) ...(iv)
From Eqs. (iii) and (iv),
ar(ΔAGB)=ar(ΔBGC)=ar(ΔAGC) ...(v)
Now,
ar(ΔABC)=ar(ΔAGB)+ar(ΔBGC)+ar(ΔAGC)
⇒ ar(ΔABC)=ar(ΔAGB)+ar(ΔAGB)+ar(ΔAGB) [from Eq. (v)]
⇒ ar(ΔABC)=3ar(ΔAGB)
⇒ ar(ΔAGB)=13ar(ΔABC) ...(vi)
From Eqs. (v) and (vi),
ar(ΔBGC)=13ar(ΔABC)
and ar(ΔAGC)=13ar(ΔABC) Hence proved.
Topper's Solved these Questions
Similar Questions
In the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
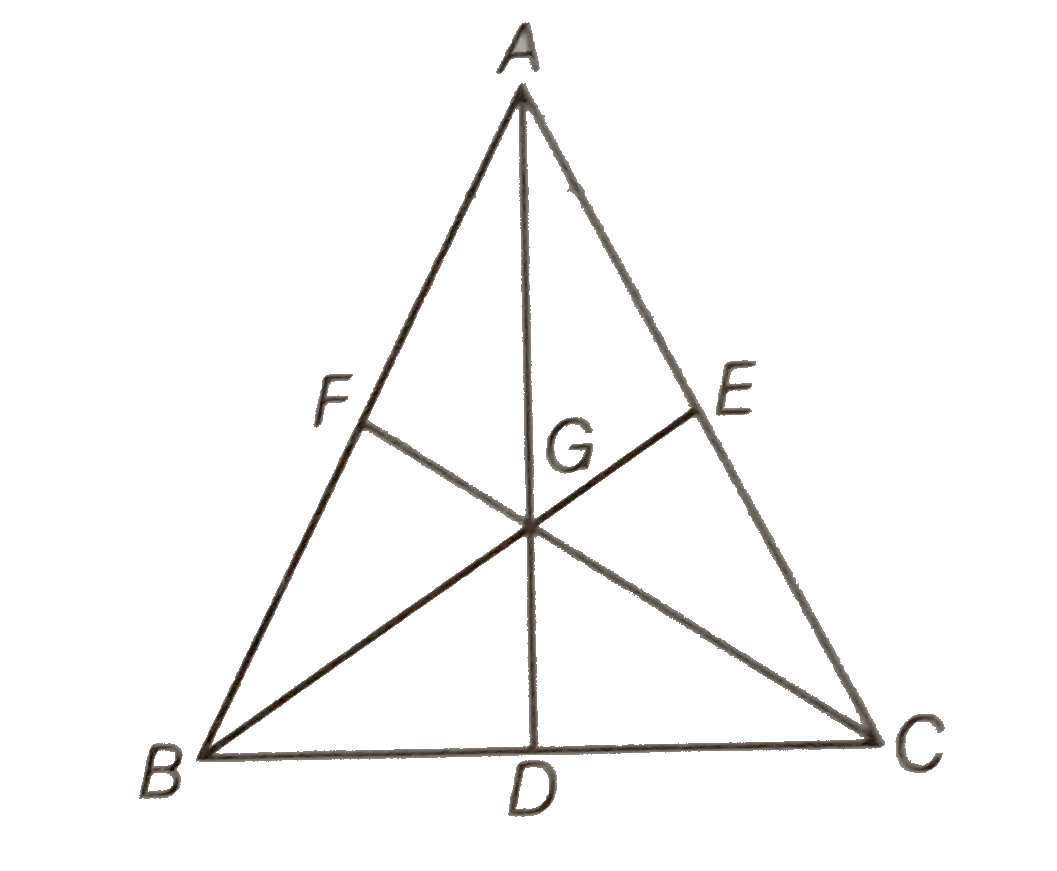
View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View Solution
Knowledge Check
If ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
A√k21+k22+k23B√k1k2k3k21+k22+k23C√∣∣(k21+k22−k23)∣∣D√∣∣(k21−k22−k23)∣∣ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.ar(△ABD)=k2,ar(△BCD)=k3, then ar(△ACD) is
A√k21+k22+k23B√k1k2k3k1+k2+k3C√∣∣k21+k22−k23∣∣D√∣∣k22−k21−k23∣∣In △ABC, P is the mid-point of BC and Q is the mid-point of AP. Find the ratio of the area of △ABQ and the area of ∠ABC. The following are the steps involved in solving the above problem.
A) We know that a a median of a triangle divides a triangle into two triangles of equal area.
B) ⇒Ar(△ABP)=12[Ar(△ABC)]
C) Ar(△ABQ)=12[Ar(△ABP)]=14[Ar(△ABC)]
D) ⇒(△ABQ):Ar(△ABC)=1:4AABCDBADBCCABCDDADCB
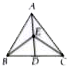
In the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
View SolutionABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.Ar(△ABD)=k2,ar(△BCD)=k3 then ar(△ACD) is
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionAD is one of the medians of a ABC..X is any point on AD . Show that ar(ABX)=ar(ACX)
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View Solution
