if the tangent at the ends B and B' of minor axis at L and L' respectively , then B:.B'.L'=
a2
b2
a2+b2
A2=b2
The correct Answer is:A
Topper's Solved these Questions
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Chapter Test
30 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type
7 Videos
- DIFFERENTIATIONBOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test
30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
Similar Questions
Knowledge Check
The lengths of the tangents from the points A and B to a circle are l1 and l2 respectively. If points are conjugate with respect to the circle, then AB2=
Al1+l2Bl21+l22C∣∣l21−l22∣∣Dnone of theseArea of a rectangle =L×B
Perimeter of a rectangle = 2(L + B) where L and B are the length and breadth of the rectangle respectively.
The area of a rectangle whose length 20 cm and breadth 15 cm isA105cm2B300cm2C35cm2D30cm2Area of a rectangle =L×B
Perimeter of a rectangle = 2(L + B) where L and B are the length and breadth of the rectangle respectively.
The breadth of a rectangle of length 4 m and area 8.4m2 isA2.1 mB1.2mC4.2m2D2.1m2
Draw the images of points A and B in line l and name them as A′ and B′ respectively. Measure AB and A′ B′. Are they equal?
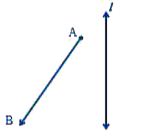
View SolutionThe figure shows the variation of photocurrent with anode potential for a photosensitve surface for three different radiations. Let la,lbandlc be the curves a, b and c, respectively

(a) fa=fbandla≠lb (b) fa=fcandla=lc
(c ) fa=fbandla=lb (d) fb=fcandlb=lc
View SolutionThe figure shows the variation of photocurrent with anode potential for a photosensitve surface for three different radiations. Let la,lbandlc be the curves a, b and c, respectively

(a) fa=fbandla≠lb (b) fa=fcandla=lc
(c ) fa=fbandla=lb (d) fb=fcandlb=lc
View SolutionTwo rigid bodies A and B rotate with rotational kinetic energies EA and EB respectively. The moments of inertia of A and B about the axis of rotation are IA and IB respectively. If IA=IB/4 and E_(A)= 100 E_(B), the ratio of angular momentum (L_(A)) of A to the angular momentum (L_(B)) of B is
View SolutionArea of a rectangle =L×B
Perimeter of a rectangle = 2(L + B) where L and B are the length and breadth of the rectangle respectively.
Find the area of a rectangular park whose perimeter is 300 and breadth is 50 m.
View Solution
