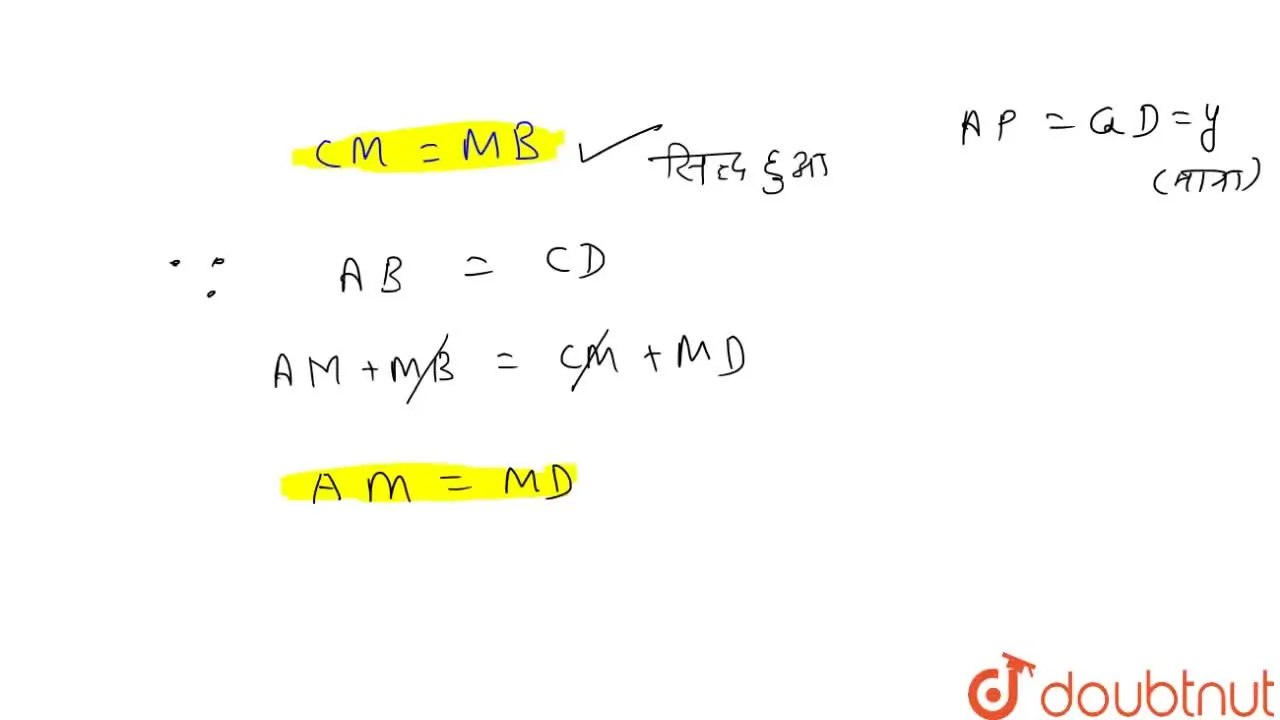
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं |
दिया है : AB तथा CD वृत्त की जीवाएँ हैं, O वृत्त का केन्द्र है | AB तथा CD, P पर प्रतिच्छेद करते हैं और AB = CD.
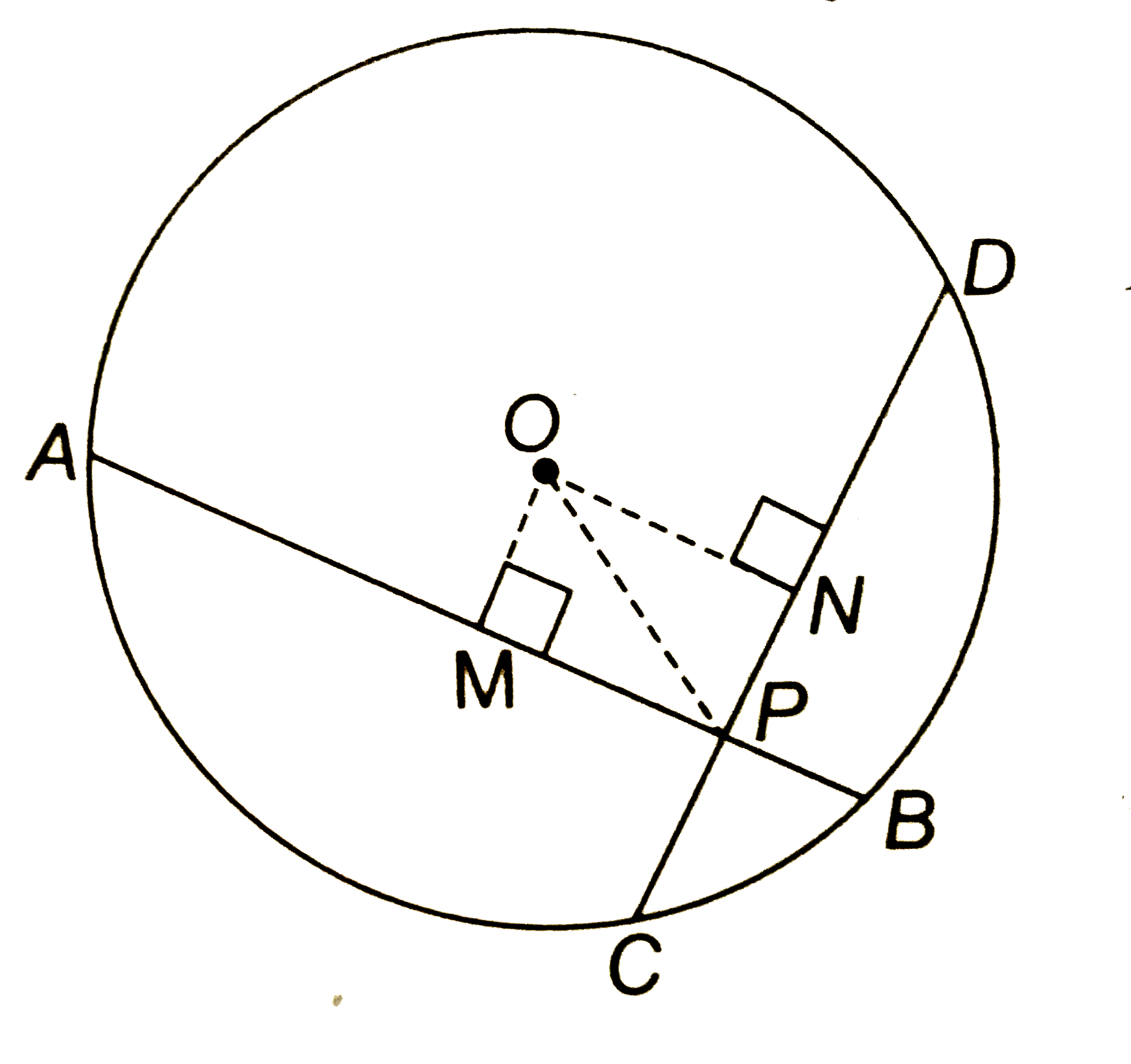
सिद्ध करना है : (i) AP = PD
(ii) PB = CP.
रचना : OM⊥AB,ON⊥CD खींचें |
OP को मिलाया |
उपपत्ति : उपपत्ति : AM=MB=12AB,
(∵ केन्द्र से जीवा पर खिंचा गया लम्ब जीवा को समद्विभाजित करता है)
CN=ND=12CD,
(∵ केन्द्र से जीवा पर खिंचा गया लम्ब जीवा को समद्विभाजित करता है)
AM=ND तथा MB=CN ...(1)
[∵AB=CD (दिया है)]
ΔOMP तथा ΔONP में,
OM=ON
(∵ एक वृत्त की समान जिवाएँ केन्द्र से समान दूरी पर स्थित होती हैं |)
∠OMP=∠ONP (∵ प्रत्येक 90∘)
OP=OP (उभयनिष्ठ)
ΔOMP≅ΔONP (R.H.S. से)
⇒ MP=PN (c.p.c.t.) ...(2)
समीकरण (1) तथा (2) को जोड़ने पर,
AM+MP=ND+PN⇒AP=PD
समीकरण (1) में से समीकरण (2) को घटाने पर
BM−MP=CN−PN⇒PB=CP
अत: (i) AP=PD और (ii) PB = CP.
Related Playlists
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.5)12videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.6 ऐच्छिक)10videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.3)3videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन5videos
रेखाएं और कोण
- BOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)10videos
संख्या पद्धति
Similar Questions
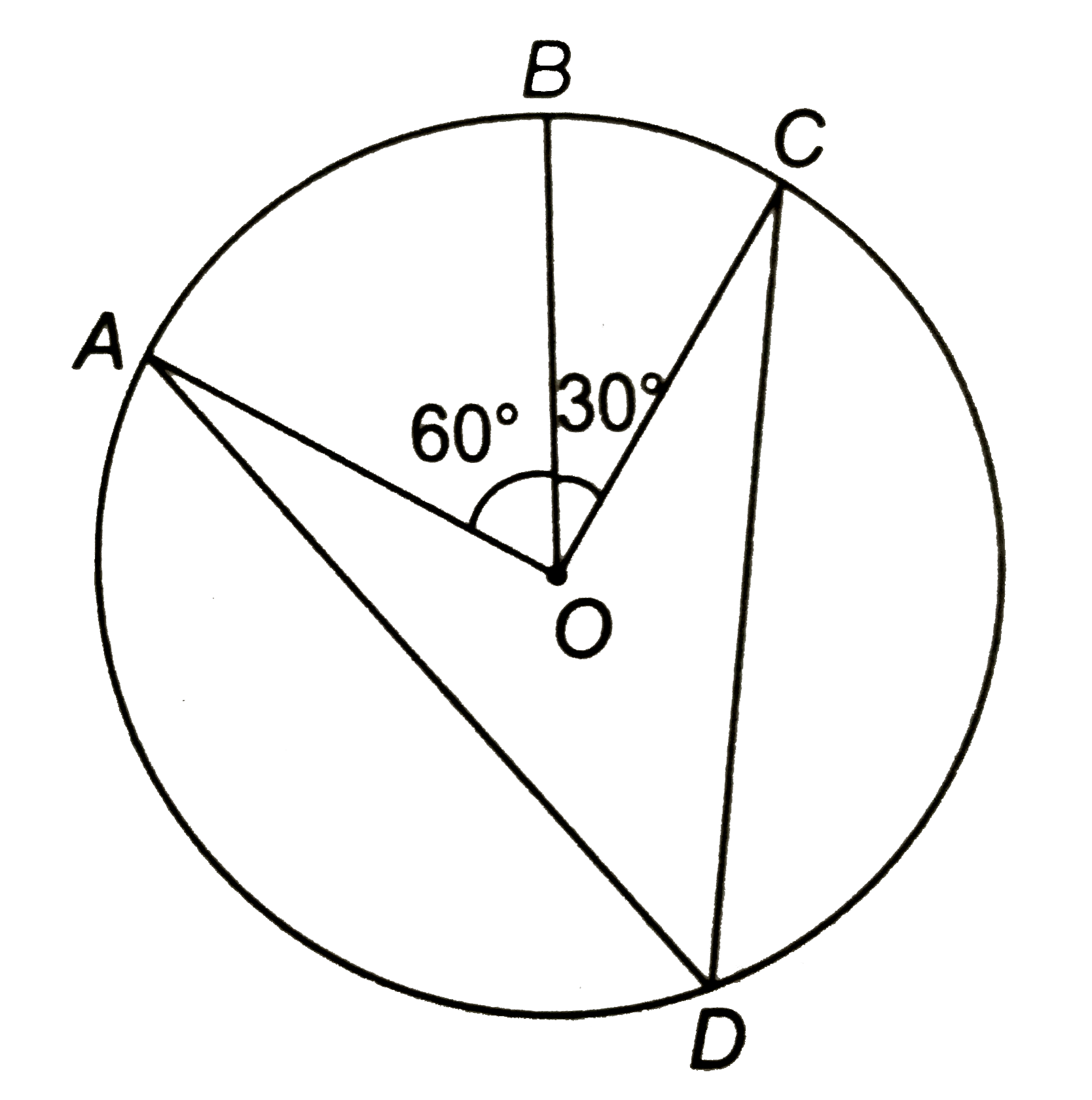
आकृति में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC=30∘ तथा ∠AOB=60∘ है | यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए |
 04:26View Solution
04:26View Solutionसिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अंतरित करती है |
02:37View Solutionवृत्तों के कई जोड़े (युग्म) खींचिए | प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं कई अधिकतम संख्या क्या है ?
 02:36View Solution
02:36View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALCView Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
02:52View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
03:00View Solutionयदि वृत्त x2+y2−8x−4y+c=0 के व्यास के एक सिरे के निर्देशांक (-3, 2) हों, तो दूसरे सिरे के निर्देशांक हैं
01:40View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
01:07:20View Solutionखण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
01:05:22View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
05:05View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
02:18View Solutionयदि कोई जीवा वृत्त के केन्द्र से गुजरती है, तो उसे ........." कहते हैं।
04:28View Solutionकिसी वृत्त के जीवा का मध्य बिंदु दिया है
04:58View Solutionएक बिंदु की शक्ति | किसी अन्य वृत्त के सापेक्ष दिए गए वृत्त की स्थिति
01:48View SolutionIn a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is: एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है:
02:48View SolutionIn a circle, two equal and parallel chords are 6 cm apart and they lie on the opposite sides of the centre of the circle, whose radius is 5 cm. The length of each chord (in cm), is एक वृत्त में, दो समान और समानान्तर जीवा 6 सेमी के दुरी पर हैं और वे वृत्त के केंद्र के विपरीत किनारों पर स्थित हैं, जिसकी त्रिज्या 5 सेमी है। प्रत्येक जीवा की लंबाई (सेमी में ) है:
02:04View Solution