If x0 is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. .Solution in Tamil
f(x0)=0
f'(x0)=0
f''(x0)=0
f''(x0)≠0
The correct Answer is:C
Step by step video, text & image solution for If x_(0) is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER - 20 (UNSOLVED)BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 20 (UNSOLVED)EXERCISE - PART - II (II. Answer any seven questions. Questions No. 30 is compulsory.)
8 Videos
- SAMPLE PAPER - 20 (UNSOLVED)BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 20 (UNSOLVED)EXERCISE - PART - III (III. Answer any seven questions. Questions No. 40 is compulsory.)
10 Videos
- SAMPLE PAPER - 2 BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 2 EXERCISE - PART -IV (Answer the questions)
11 Videos
- SAMPLE PAPER - 5BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 5EXERCISE - PART -IV
13 Videos
Similar Questions
Find the rank of the following matrices by row reduction method :
⎡⎢⎣3−85 22−51 4−1 23−2⎤⎥⎦
View SolutionA chemist has one solution which is 50% acid and another solution which is 25 % acid. How much each should be mixed to make 10 litres of a 40 % acid solution ? (Use Cramer's rule to solve the problem).
View SolutionIf F(α)=⎡⎢⎣cosα0sinα010−sinα0cosα⎤⎥⎦, show that [F(α]−1=F(−α).
View SolutionAn amount of Rs 65,000 is invested in three bonds at the rates of 6 % , 8% and 10% per annum respectively. The total annual income is Rs 4,800. The income from the third bond is Rs 600 more than that from the second bond. Determine the price of each bond. (Use Gaussian elimination method. )
View SolutionThe area bounded by the curve y=xe^(-x);xy=0 and x=c where c is the x - coordinate of the curve's inflection point,is
View SolutionThe graph of the derivative f of a continuous function f is shown with f(0)=0

If f(x) has local minima at x=x1 and x=x2,f has inflection point at x=k, number of critical points of y=f(x) is w then x1+x2−k−w is...........
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
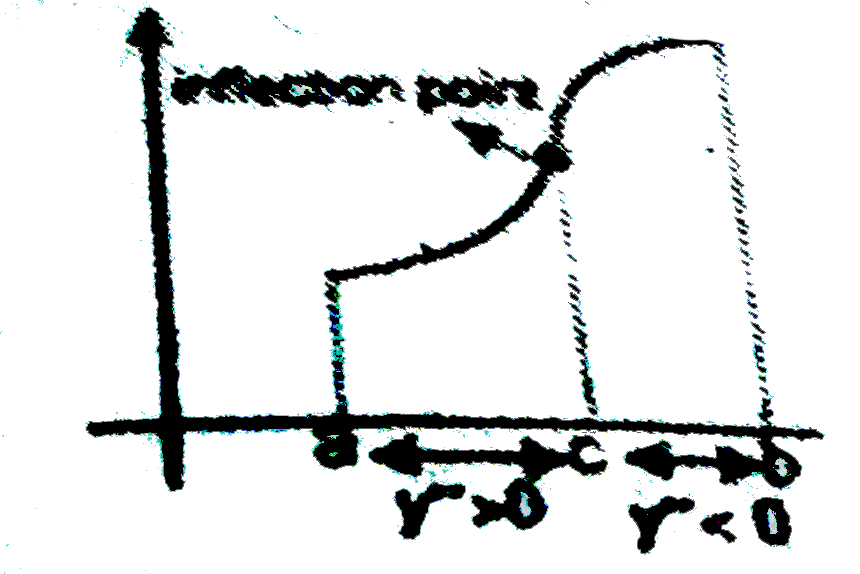
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionThe point of inflection of the curve y=(x−1)3 is
View SolutionThe point of inflection of the curve y=x4 is at:
View SolutionA point of inflection of the curve y=e−x2 is
View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
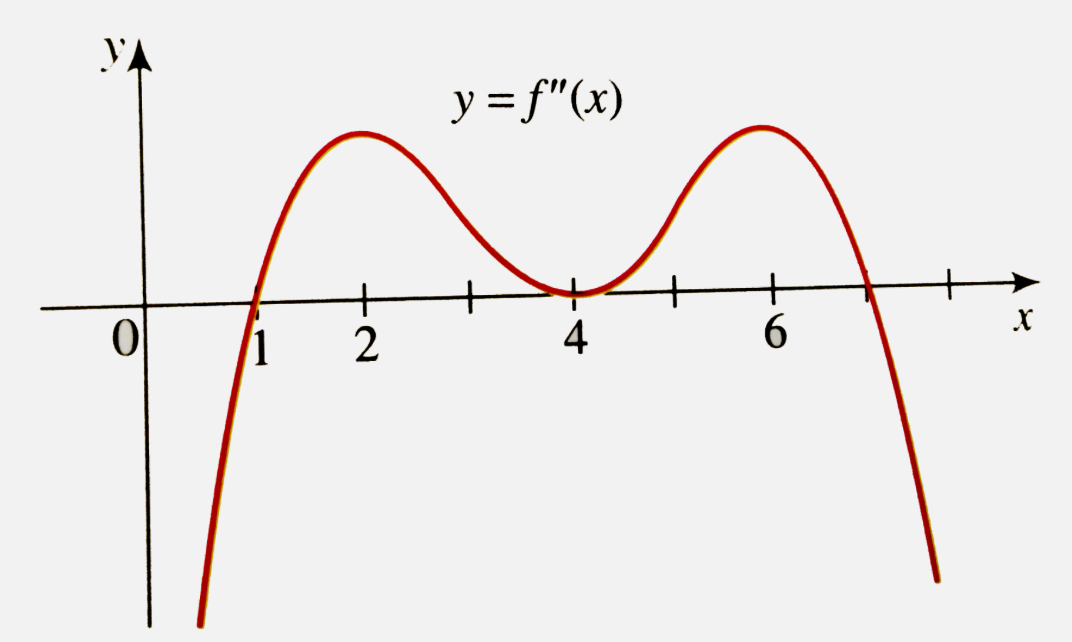
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionIf f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
If y=x4+x3−18x2+24x−12 then
View SolutionIf f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
If y=x4+x3−18x2+24x−12 then
View Solution
