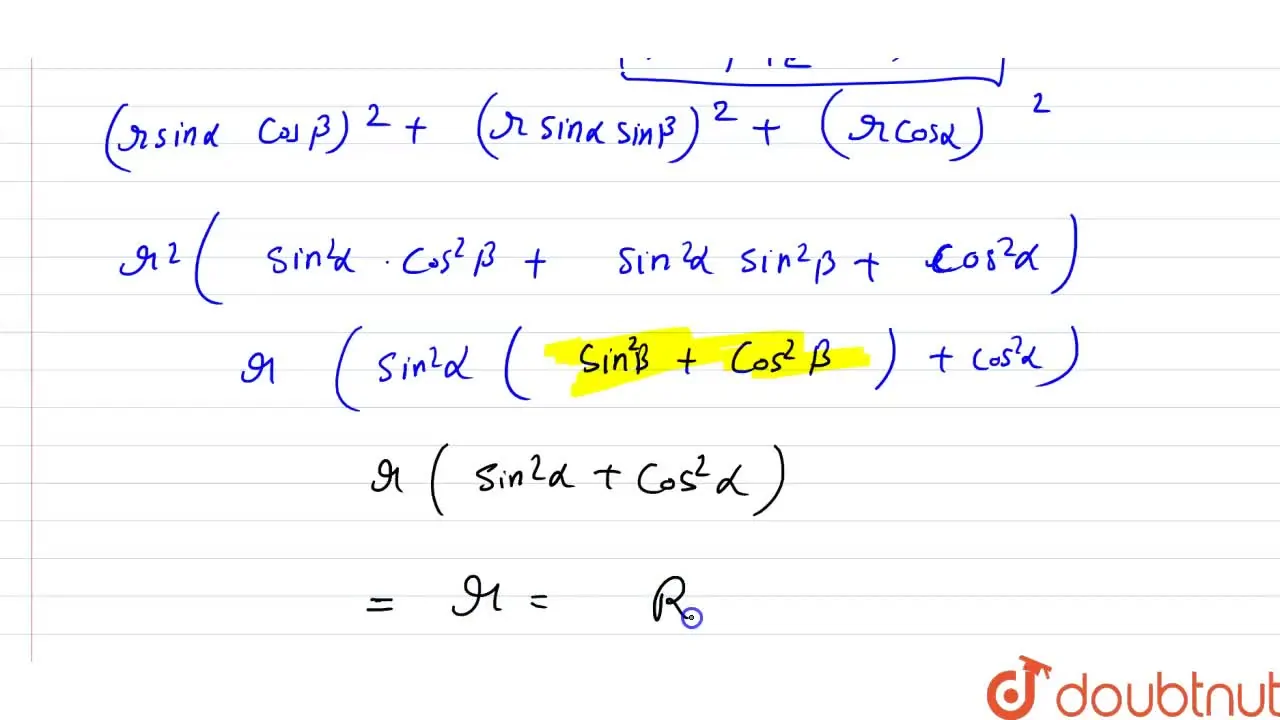If x=rsinαcosβ,y=rsinαsinβandz=rcosα, prove that
x2+y2+z2=r2.
Video Solution
Text Solution
We have
x2+y2+z2=r2sin2αcos2β+r2sin2αsin2β+r2cos2α
=r2sin2α(cos2β+sin2β)+r2cos2α
=r2sin2α+r2cos2α [∵cos2β+sin2β=1]
=r2(sin2α+cos2α)=r2 [∵sin2α+cos2α=1].
Hence, (x2+y2+z2)=r2.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13A38videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13B15videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 1035videos
TRIGONOMETRIC RATIOS
Similar Questions
If x=rcosαcosβ,y=rcosαsinβ,z=rsinα then x2+y2+z2=
View SolutionIf x=sinα,y=sinβ,z=sin(α+β) then cos(α+β)=
View SolutionIf cosα+cosβ=0=sinα+sinβ, then cos2α+cos2β=
View SolutionIf x=rcosαcosβ,y=rcosαsinβ,z=rsinα then x2+y2+z2=
View SolutionIf cosα+cosβ=0=sinα+sinβ then cos2α+cos2β=
View SolutionProve that (cosα+cosβ)2+(sinα+sinβ)2=4cos2(α−β2).
View Solution(cosα−cosβ)2+(sinα−sinβ)2=
View SolutionIf cosα+cosβ=0=sinα+sinβ, then value of cos2α+cos2β is
View SolutionIf x=rsinAcosC, y=rsinAsinC and z=rcosA , prove that r2=x2+y2+z2
View Solution(cosα+cosβ)2+(sinα+sinβ)2=
View Solution