In a class test, the sum of the marks obtained by P in Mathematics and science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of his marks, would have been 180. Find his marks in the two subjects.
To solve the problem, we will set up equations based on the information given in the question.
Step 1: Define Variables
Let:
- m = marks obtained in Mathematics
- s = marks obtained in Science
Step 2: Set Up the First Equation
According to the problem, the sum of the marks in Mathematics and Science is 28. Therefore, we can write the first equation as:
m+s=28
This is our Equation 1.
Step 3: Set Up the Second Equation
The problem states that if P had scored 3 more marks in Mathematics and 4 less in Science, the product of his marks would have been 180. We can express this as:
(m+3)(s−4)=180
This is our Equation 2.
Step 4: Substitute s from Equation 1 into Equation 2
From Equation 1, we can express s in terms of m:
s=28−m
Now, substitute this expression for s into Equation 2:
(m+3)((28−m)−4)=180
Simplifying the equation gives:
(m+3)(24−m)=180
Step 5: Expand the Equation
Now, we will expand the left side:
m⋅24−m2+72−3m=180
This simplifies to:
24m−m2+72−3m=180
Combining like terms:
21m−m2+72=180
Step 6: Rearrange the Equation
Now, we will rearrange the equation to set it to zero:
−m2+21m+72−180=0
This simplifies to:
−m2+21m−108=0
Multiplying through by -1 gives:
m2−21m+108=0
Step 7: Factor the Quadratic Equation
Now we will factor the quadratic equation:
(m−12)(m−9)=0
Setting each factor to zero gives us:
1. m−12=0 → m=12
2. m−9=0 → m=9
Step 8: Find Corresponding Values of s
Now we will find the corresponding values of s using Equation 1:
1. If m=12:
s=28−12=16
2. If m=9:
s=28−9=19
Final Results
Thus, the marks obtained by P in the two subjects can be:
1. Mathematics: 12, Science: 16
2. Mathematics: 9, Science: 19
Let:
- m = marks obtained in Mathematics
- s = marks obtained in Science
According to the problem, the sum of the marks in Mathematics and Science is 28. Therefore, we can write the first equation as:
m+s=28
This is our Equation 1.
The problem states that if P had scored 3 more marks in Mathematics and 4 less in Science, the product of his marks would have been 180. We can express this as:
(m+3)(s−4)=180
This is our Equation 2.
From Equation 1, we can express s in terms of m:
s=28−m
Now, substitute this expression for s into Equation 2:
(m+3)((28−m)−4)=180
Simplifying the equation gives:
(m+3)(24−m)=180
Now, we will expand the left side:
m⋅24−m2+72−3m=180
This simplifies to:
24m−m2+72−3m=180
Combining like terms:
21m−m2+72=180
Now, we will rearrange the equation to set it to zero:
−m2+21m+72−180=0
This simplifies to:
−m2+21m−108=0
Multiplying through by -1 gives:
m2−21m+108=0
Now we will factor the quadratic equation:
(m−12)(m−9)=0
Setting each factor to zero gives us:
1. m−12=0 → m=12
2. m−9=0 → m=9
Now we will find the corresponding values of s using Equation 1:
1. If m=12:
s=28−12=16
2. If m=9:
s=28−9=19
Thus, the marks obtained by P in the two subjects can be:
1. Mathematics: 12, Science: 16
2. Mathematics: 9, Science: 19
Topper's Solved these Questions
Similar Questions
In a class test, the sum of Shefalis marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
View SolutionIn a class test, the sum of Shefalis marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
View Solution
Knowledge Check
Raza scored 30 marks in Maths, x marks in Science and y marks in English. What is his total score in these three subjects ?
A30+x+yB30+x−yCx+y−30D30+30x+30y
Anjali scores 100 marks in Mathematics and x marks in Science. what is her total score in Science and Mathematics?
View SolutionRahim obtained 60 marks out of 75 in Mathematics. Find the percentage of marks obtained by Rahim in Mathematics.
View SolutionThe table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
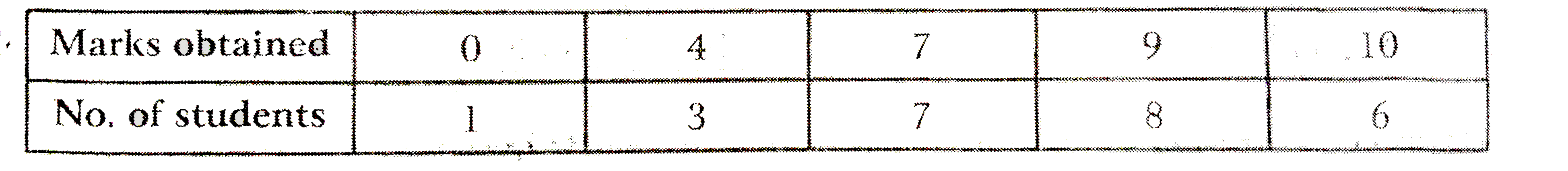
View SolutionSunny scored x marks in Maths, y marks in Science and 50 marks in English. What is his total score in these three subjects?
View SolutionIn Figure, the pie-chart shows the marks obtained by a student in various subjects. If the student scored 135 marks in mathematics, find the total marks in all the subject. Also, find his score in individual subjects.
View SolutionRahul scores 80 marks in English and x marks in Hindi. What is his total score in the two subjects?
View SolutionSaina secure 70 marks in Science and 80 marks in Mathematics. Find
a. the ratio of Sania's marks in Science to her marks in Mathematics.
b. the ratio of Sania's marks in Mathematics to her marks is Science.
View Solution
