In a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid-point of AC. If AB+2AD+BC-2 DC=k PQ, then k is equal to
−6
−4
6
4
The correct Answer is:A
Now, AB+2AD+BC−2DC
=AC+2AD−2DC [∵AB+BC=AC]
=AC+2(AC+CD)−2DC
=3AC−4DC
=3(2QC)−4(32PC)
=6QC−6PC
=6(QC+CP)
⇒kPQ=6QP=−6PQ [given]
implies k = - 6

Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - VECTORS EXERCISE - (VECTORS ) Exercise 2 ( Topical problems )88videos
VECTORS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - VECTORS EXERCISE - ( MHT CET Corner)66videos
VECTORS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESEXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)20videos
TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal toA2/3B1/3C1/2D3/4 - Question 2 - Select One
Area of quadrilateral ACDE is 36cm2, B is the mid-point of AC. Find the area of ΔABE if AC||DEandBE||DC :
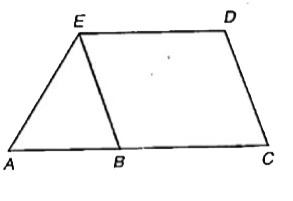 A10cm2B9cm2C12cm2Dcan't be determined
A10cm2B9cm2C12cm2Dcan't be determined - Question 3 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratioA1:2B1:3C3:1D2:1
In Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
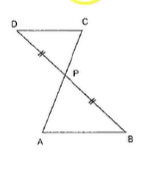 View Solution
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
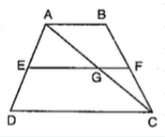 View Solution
View SolutionDiagonals of a quadrilateral ABCD intersect in point Q. if 2 QA = QC, 2 QB = QD, then prove that DC = 2 AB.
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratioView Solution

