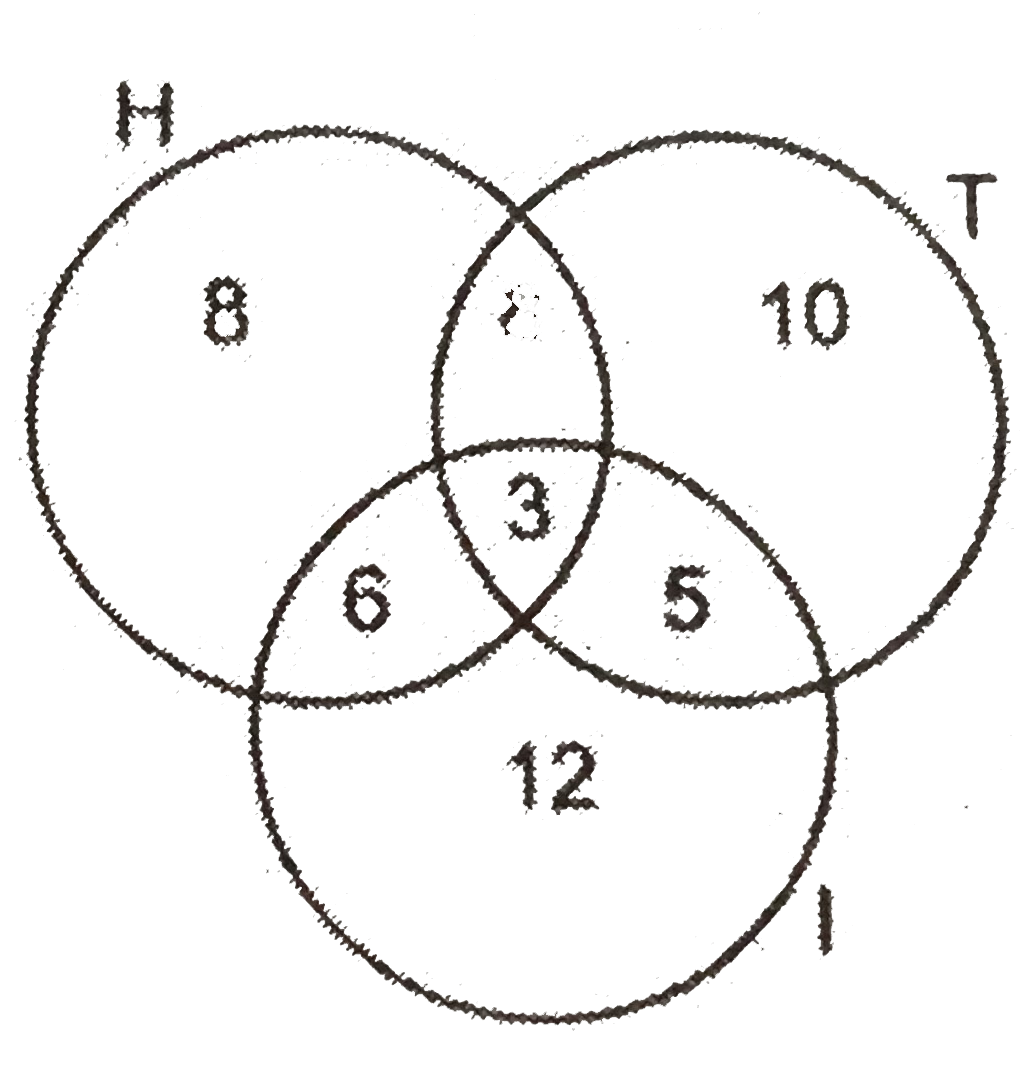
In a survey of 60 people, it was found that 25 people read newspaper H. 26 read newspaper T, 26 read newspaper 1, 9 read both H and I. 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find: (i) the number of people who read at least one of the newspapers. (ii) the number of people who read exactly one newspaper
Let number of people read newspaper H is , newspaper T is and newspaper is
(i) Number of people who read at least one newspaper will be
then
Therefore, 52 people read at least one newspaper.
(ii) Number of people who read newspaper H and T only
Similarly, number of people who read newspaper T and I only
and number of people read newspaper H and I only
Therefore, number of people who read only two newspaper
These are not included the people who read three newspaper
Therefore, number of people who read at least two newspaper = number of people who read two + three newspaper
Number of people who read only one newspaper
Therefore, 30 people read only one newspaper.
Topper's Solved these Questions
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1.6
8 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
Similar Questions
In a survey of 60 persons, it is found that 25 read newspaper H, 26 read T, 26 read I, 9 read H and I, 11 and H and T,8 read T and I and 3 read all three newspaper. Find :
(a) No. of persons who read atleast one newspaper.
(b) No. of persons who read exactly one newspaper.
View SolutionIn a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10 % families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4 % buy a and C. If 2% families buy all the three newspaper. Find
(i) the number of families which buy newspaper A only.
(ii) the number of families which buy none of A , B and C.
View Solution
Knowledge Check
In a hostel, 60% of the students read Hindi newspaper, 40% read English newspaper and 20% read both Hindi and English newspaper. A student is selected at random, if she reads Hindi newspaper, then the probability she reads English newspaper is
A12B13C23DNone of theseIn a town of 840 persons, 450 persons read Hindi, 300 read English and 200, read both. The number of persons who read neither is
A(a) 210B(b) 290C(c) 180D(d) 260
In a survey of 100 persons it was sound that 28 read magazine A, 30 readmagazine B, 42 read magazine C, 8 read magazines A & B, 10 read magazine A & C and 5 read magazine B&C and 3 read all the three. Find how many read none of three magazines?
View SolutionIn a city, three daily newspapers A,B,C are published. 42% of the people in that city read A, 51% read B and 68% read C. 30% read A and B, 28% read B and C ,36%read A and C. 8% do not read any of the three newspapers. The percentage of persons who read all the three papers is
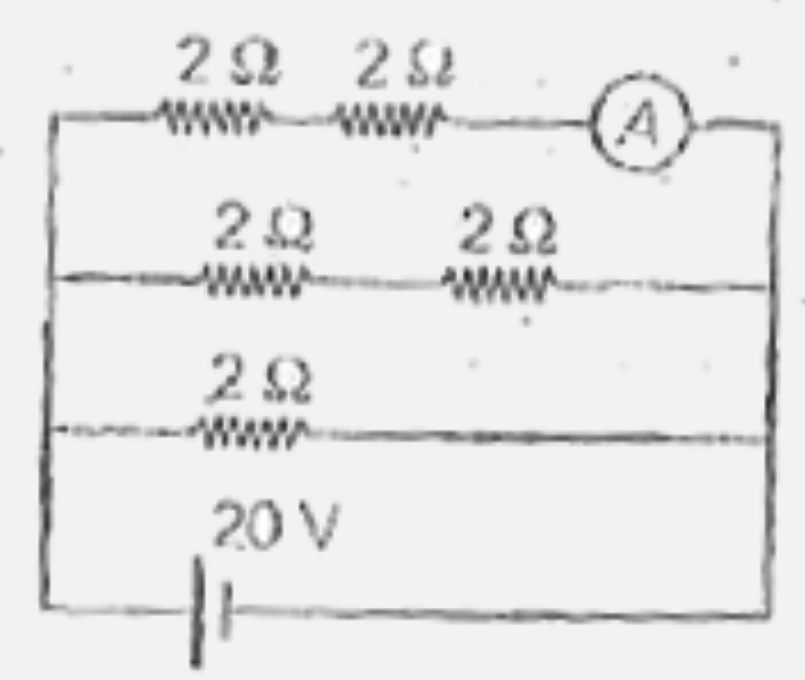
View SolutionThe reading of the ammeter in the circuit below is
View SolutionIn a town of 840 persons , 450 persons read Hindi, 300 read English and 200 read both. Then, the number of persons who read neither, is
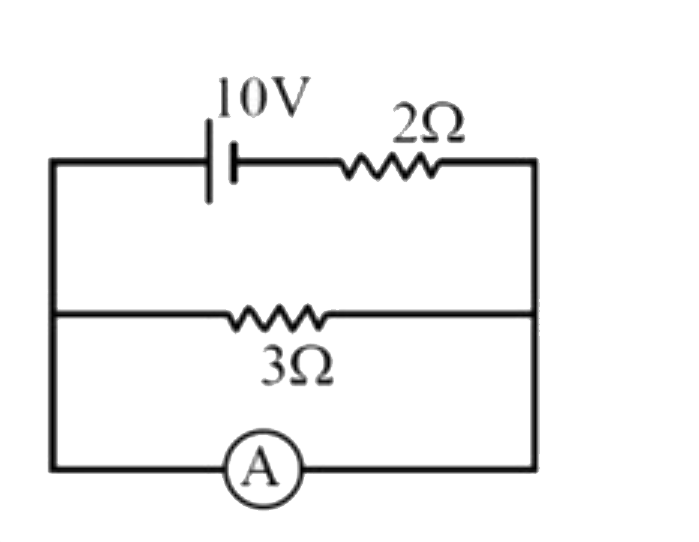
View SolutionThe reading of the ideal ammeter in the circuit is
View SolutionTimes, Mirror and Sun are three newspapers All readers of the Times read the Sun. Every person either reads the Sun or does not read the Mirror. 11 people read the Sun but does not read the Mirror. 8 people read either the Times or the Mirror but not both. 10 people read the Sun and either read the Mirror or do not read the Times. 14 people either read the Sun and not the Mirror or read both the Sun and Mirror. 9 people neither read the Times nor the Mirror. Number of people who read Times and Mirror both are
View Solution
