In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
a:b
(3a+b):(a+3b)
(a+3b):(3a+b)
(2a+b):(3a+b)
The correct Answer is:B
Given, AB = a cm, DC = b cm and AB|| DC.
Also, E and F are mid-points of AD and BC, respectively.
So, distance between CD, EF and AB, EF will be same say h.
Join BD which intersect EF at M.
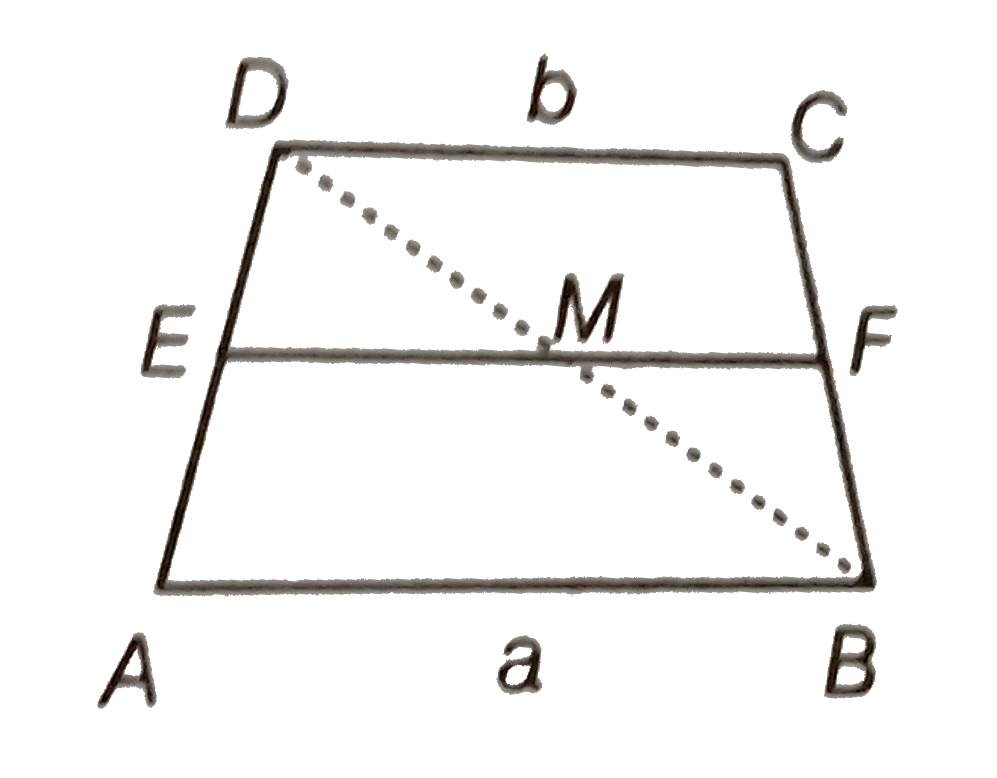
Now, in ΔABD,E is the mid-point of AD and EM || AB
So, M is the mid-point of BD
and EM=12AB [by mid-point theorem] ...(i)
Similarly in ΔCBD , MF=12CD ...(ii)
On adding, Eqs. (i) and (ii), we get
EM+MF=12AB+12CD
⇒ EF=12(AB+CD)=12(a+b)
Now, area of trapezium ABFE=12(sum of parallel sides)×(distance between parallel sides)
=12(a+12(a+b))×h=14(3a+b)h
Now, area of trapezium EFCD =12[b+12(a+b)]×h=14(3b+a)h
∴ Required ratio=Area of ABFEArea of EFCD=14(3a+b)H14(3b+a)H
=(3a+b)(a+3b)or (3a+b):(a+3b)
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions
5 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.3 Short Answer Type Questions
9 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=A40 cmB50 cmC60 cmD30 cm
The figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
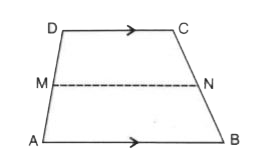
MN, if AB = 11 cm and DC = 8 cm.
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
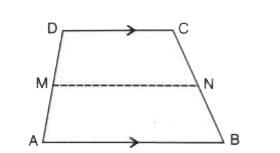
AB, if DC = 20 cm and MN = 27 cm
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
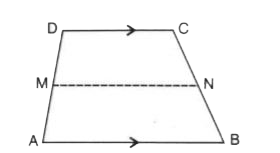
DC, if MN = 15 cm and AB = 23 cm.
View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
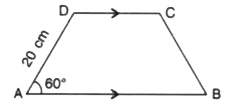
(i) length of AB
View Solution
