In a triangle ABC, right angled at A, on the leg AC as diameter, semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals toSolution in Bengali
The correct Answer is:D
Step by step video, text & image solution for In a triangle ABC, right angled at A, on the leg AC as diameter, semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC equals to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Divide the join of points P(2, 5) and Q(-7, 4) in the ratio 1 : 2
internally
View SolutionIf x=−5+2√−4, find the value of x2+4.
View SolutionIn a right triangle ABC ,right angled at A, on the leg AC as diameter,a semicircle is described.The chord joining A with the point of intersection D of the hypotenuse and the semicircle,then the length AC equals to
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
View SolutionLet ABC be a right triangle with length of side AB=3 and hypotenuse AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter,a semicircle is described.If a chord joi A with the point of intersection D of the hypotenuse and the semicircle,then the length of AC equals to
View SolutionABC is a right angle in a right triangle ABC. If the line drawn parallel to BC through the hypotenuse AB denominator M intersects AC at D, then prove the following point AC midpoint D
View Solution∠ACB is an angle in the semicircle of diameter AB =5 and AC : BC = 3 : 4 The area of the triangle ABC is
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View Solutionangle A At right angles Delta ABC Assuming the side AC of the diameter to be drawn, a semicircle is drawn. If a chord connects the point and the intersection of the hypotenuse and the semicircle of the triangle, then the length of the side AC is
View SolutionIn a triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semicircle, then the length of AC is equal to AB.AD√AB2+AD2 (b) AB.ADAB+AD √AB.AD (d) AB.AD√AB2−AD2
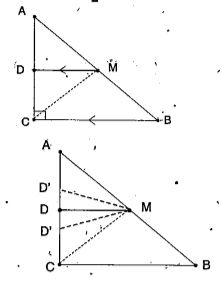
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View Solutionएक समकोण त्रिभुज ABC के कर्ण AC का मध्य बिन्दु D है तो सिद्ध करें कि BD=12AC

View SolutionABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : D is the midpoint of AC.
View Solution
