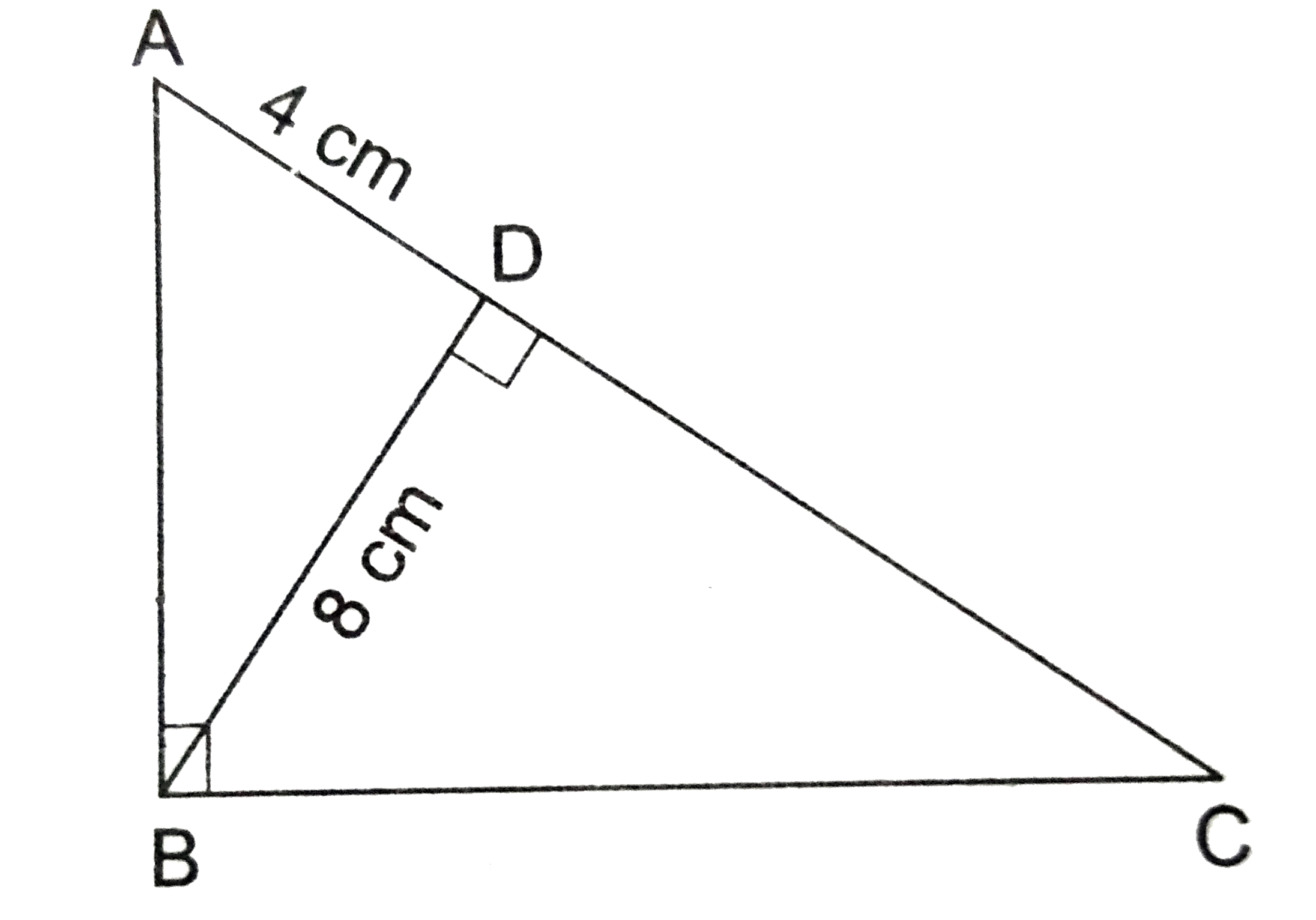
In an isosceles right triangle ABC, ∠B=90∘ and ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC.Then BD=………………(AB2/BC2/AC2).
Video Solution
Text Solution
AC2
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CONCEPT APPLICATION
61 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CONCEPT APPLICATION
61 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘ABC is a right triangle with ∠B=90∘ and AC - AB = 1. If BC=√n then AB is
An+12Bn−12Cn2Dn−32In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD

In right -angled △ABC,BD⊥AC.
If AD =4 DC =9 then find BD.
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
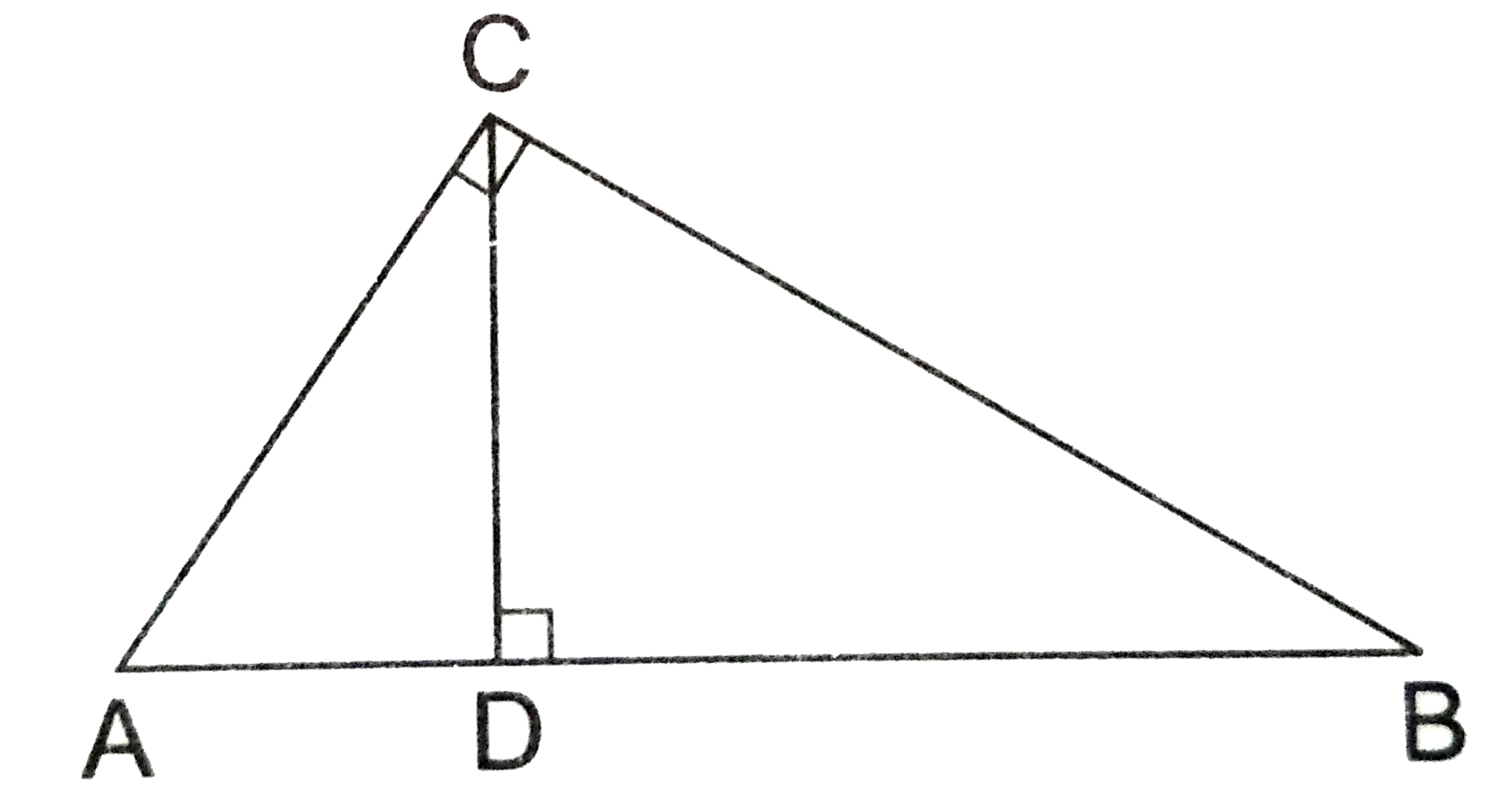
View SolutionABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
View SolutionIn an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
View SolutionIn ΔABC,∠B=90∘ and BD⊥AC. If AC = 9 cm and AD = 3 cm, then BD is equal to :
View Solution