In example 70, equations of the sides QR and RP are respectively
y=2√3x+1andy=−2√3x−1
y=x√3andy=0
y=√32x+1andy=−√32x−1
y=√3xandy=0
The correct Answer is:D
Clearly, RP is along x-axis.
So, its equation is y=0.
The equation of QR is y =√3x.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
Similar Questions
In A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
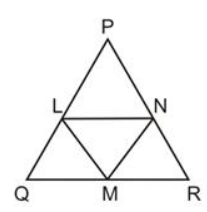 View Solution
View SolutionLet O be the origin and−−→OX,−−→OY,−−→OZ be three unit vector in the directions of the sides −−→QR,−−→RP,−−→PQ respectively , of a triangle PQR.
∣∣∣−−→OX×−−→OY∣∣∣=View Solution
Knowledge Check
- Question 1 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3 - Question 2 - Select One
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM - Question 3 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
In a triangle PQR, P is the largest angle and cosP=13. Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
View SolutionIn a triangle PQR, P is the largest angle and cosP=13. Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
View SolutionA circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
Equations of the sides QR, RP areView SolutionLet O be the origin and−−→OX,−−→OY,−−→OZ be three unit vector in the directions of the sides −−→QR,−−→RP,−−→PQ respectively , of a triangle PQR.
∣∣∣−−→OX×−−→OY∣∣∣=View SolutionIn a triangle PQR, P is the largest angle and cosP=1/3. Further the incircle of the triangle touches the sides PQ. QR and PR at N, L and M, respectively, such that the length of PN, QL, and RM are consecutive even integers. Then possible length (s) of the side(s) of the triangle is (are)
View Solution

