Question

In Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) $\Delta AEP~\Delta CDP$ (ii) $\Delta ABD~\Delta CBE$ (iii) $\Delta AEP~\Delta ADB$(iv) $\Delta PDC~\Delta BEC$

Explanation

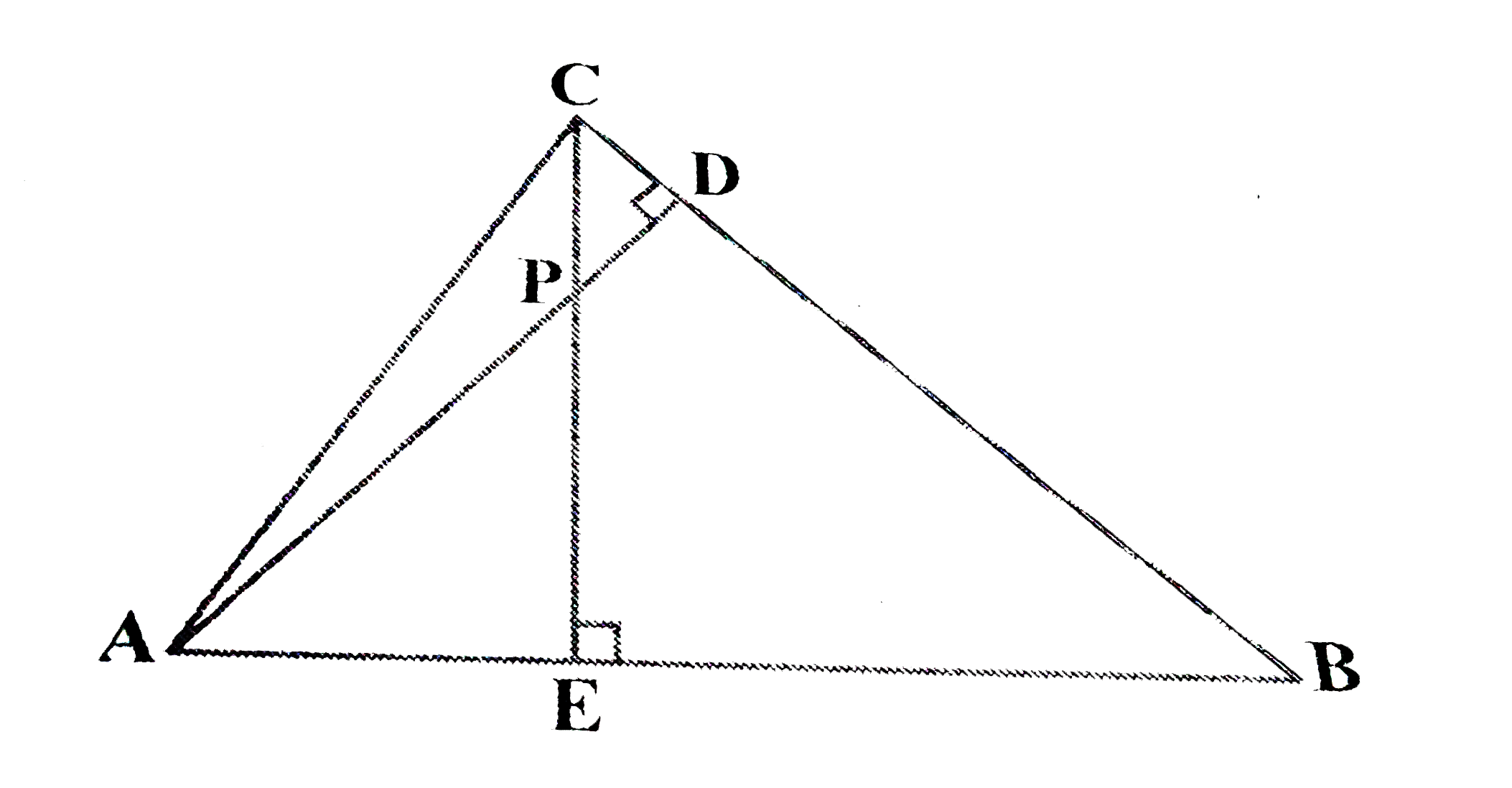
Data: altitudes AD and CE of ABC Intersect each other at the point P.
To Prove: (i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
(i) In ∆AEP and ∆CDP. ∠AEP = ∠CDP = 90° (data)
∠APE = ∠CPD (Vertically opposite angle)
∴ ∠PAE = ∠PCD
These are equiangular triangles.
Similarity criterion for ∆ is A.A.A
∴ ∆AEP ~ ∆CDP
(ii) In ∆ABD and ∆CBE. ∠ADB = ∠CEB = 90° (data)
∠ABD = ∠CBE (common)
∴ ∠DAB = ∠BCE
These are equiangular triangles.
∴ Similarity criterion for is A.A.A.
∴ ∆ABD ~ ∆CBE
(iii) In ∆AEP and ∆ADB.
∠AEB = ∠ADB = 90° (data)
∠PAE = ∠DAB (common)
∴ ∠APE = ∠ABD.
∴ These are equiangular triangles.
∴ Similarity criterion for is A.A.A.
∴ ∆AEP ~ ∆ADB
(iv) In ∆PDC and ∆BEC.
∠PDC = ∠BEC = 90° (data)
∠PCD = ∠BCE (common) ∴
∠CPD = ∠CBE
∴ These are equiangular angular triangles.
Similarity criterion for ∆ is A.A.A.
∴ ∆PDC ~ ∆BEC.