In figure, prove that (AM+BM+CM+DM)>(AO+BO+CO+DO)

Video Solution
|
Answer
Step by step video & image solution for In figure, prove that (AM+BM+CM+DM) gt (AO+BO+CO+DO) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.1)14videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.2)9videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - OLYMPAID/ HOTS CORNER10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A0.042361111111111B0.043055555555556C0.04375D0.044444444444444
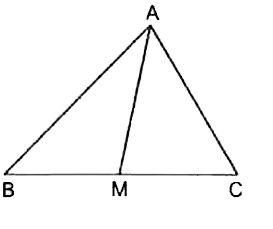
AM is median of △ABC, prove that (AB+BC+CA)>2AM.
 View Solution
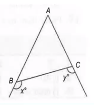
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
 View Solution
View SolutionIn ΔABC prove that AB2+AC2=2(AO2+BO2); where O is the middle point of BC.
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
 View Solution
View SolutionIn ABC Prove that AB2+AC2=2(AO2+BO2) , where O is the middle point of BC
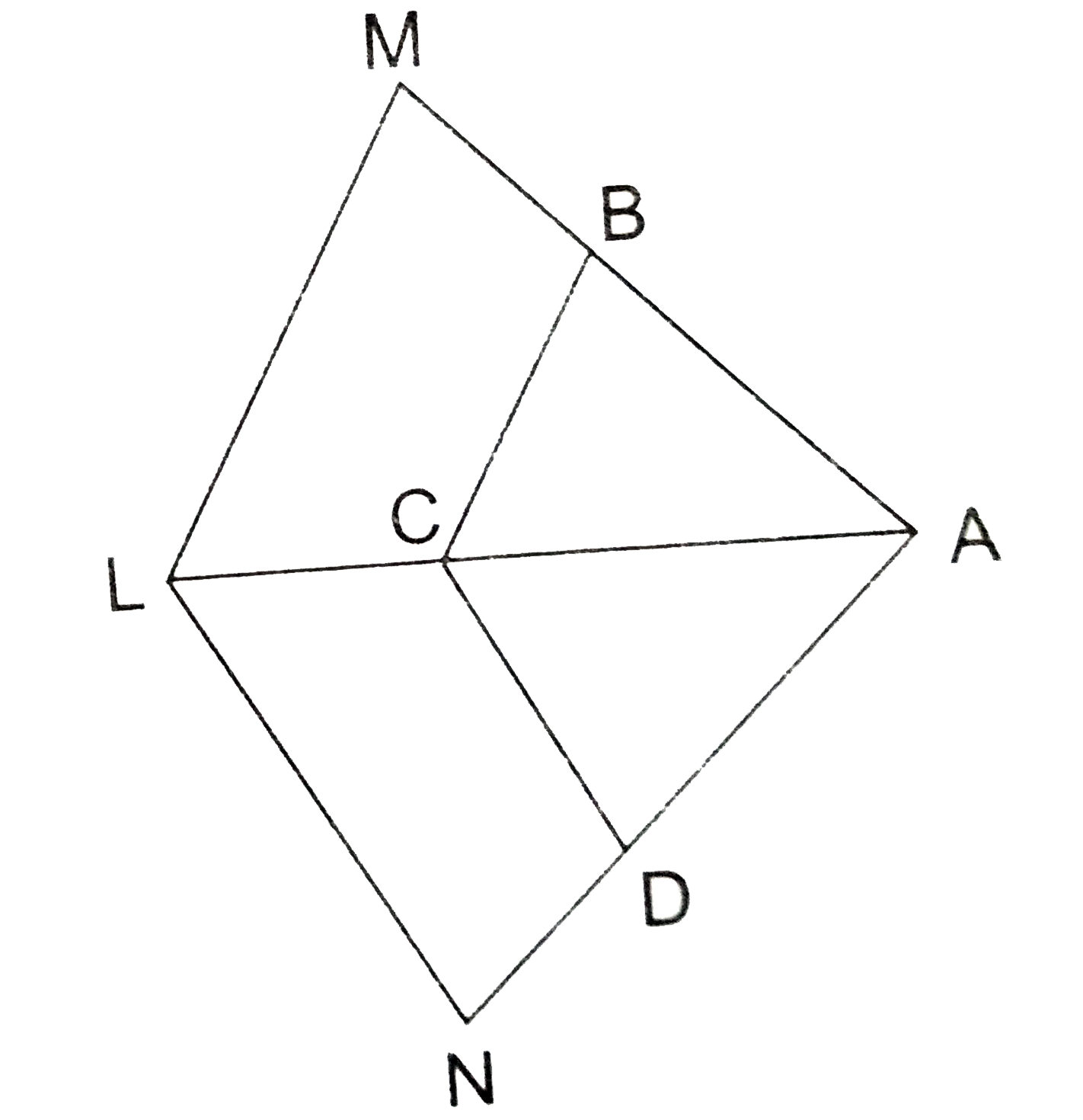
View SolutionIn the given figure, LM||CB||andLN∣∣CD.
Prove that AMAB=ANAD
 View Solution
View SolutionIn the given figure, we have AO = BO and CO = DO. Prove that ΔAOC≅ΔBOD.
 View Solution
View Solution