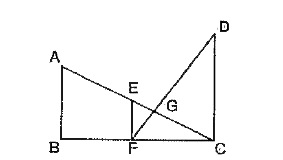
In rectangle ABCD, AB = 5 cm and BC = 3 cm. Point F and G are on the line segment CD so that DF = 1 cm and GC = 2 cm. Lines AF and BG intersect at. E. What is the area of AEB ?
10 sq. cm
152 sq. cm
25/2 sq. cm
20 sq. cm
The correct Answer is:C
To solve the problem step by step, let's break it down:
Step 1: Understand the Rectangle and Points
- We have rectangle ABCD where AB = 5 cm and BC = 3 cm.
- Points F and G are on line segment CD such that DF = 1 cm and GC = 2 cm.
- Therefore, CF = CD - DF = 5 cm - 1 cm = 4 cm.
- And, DG = CD - GC = 5 cm - 2 cm = 3 cm.
Step 2: Determine the Coordinates
- Assign coordinates to the rectangle:
- A(0, 0)
- B(5, 0)
- C(5, 3)
- D(0, 3)
- Point F on CD is at (1, 3) (since DF = 1 cm).
- Point G on CD is at (3, 3) (since GC = 2 cm).
Step 3: Find the Equations of Lines AF and BG
- The slope of line AF (from A to F):
- Slope = (y2 - y1) / (x2 - x1) = (3 - 0) / (1 - 0) = 3.
- Equation of line AF: y = 3x.
- The slope of line BG (from B to G):
- Slope = (y2 - y1) / (x2 - x1) = (3 - 0) / (3 - 5) = -3/2.
- Equation of line BG: y - 0 = (-3/2)(x - 5) → y = (-3/2)x + (15/2).
Step 4: Find the Intersection Point E
- Set the equations of AF and BG equal to find E:
- 3x = (-3/2)x + (15/2).
- Multiply through by 2 to eliminate the fraction: 6x = -3x + 15.
- Combine like terms: 9x = 15 → x = 15/9 = 5/3.
- Substitute x = 5/3 into y = 3x to find y:
- y = 3(5/3) = 5.
- Therefore, point E is at (5/3, 5).
Step 5: Calculate the Area of Triangle AEB
- The area of triangle AEB can be calculated using the formula:
Area=12×base×height
- Here, base AB = 5 cm and height is the y-coordinate of point E, which is 5 cm.
- Thus, the area is:
Area=12×5×5=252 cm2.
Final Answer
The area of triangle AEB is 252 cm2.
---
- We have rectangle ABCD where AB = 5 cm and BC = 3 cm.
- Points F and G are on line segment CD such that DF = 1 cm and GC = 2 cm.
- Therefore, CF = CD - DF = 5 cm - 1 cm = 4 cm.
- And, DG = CD - GC = 5 cm - 2 cm = 3 cm.
- Assign coordinates to the rectangle:
- A(0, 0)
- B(5, 0)
- C(5, 3)
- D(0, 3)
- Point F on CD is at (1, 3) (since DF = 1 cm).
- Point G on CD is at (3, 3) (since GC = 2 cm).
- The slope of line AF (from A to F):
- Slope = (y2 - y1) / (x2 - x1) = (3 - 0) / (1 - 0) = 3.
- Equation of line AF: y = 3x.
- Slope = (y2 - y1) / (x2 - x1) = (3 - 0) / (3 - 5) = -3/2.
- Equation of line BG: y - 0 = (-3/2)(x - 5) → y = (-3/2)x + (15/2).
- Set the equations of AF and BG equal to find E:
- 3x = (-3/2)x + (15/2).
- Multiply through by 2 to eliminate the fraction: 6x = -3x + 15.
- Combine like terms: 9x = 15 → x = 15/9 = 5/3.
- Substitute x = 5/3 into y = 3x to find y:
- y = 3(5/3) = 5.
- Therefore, point E is at (5/3, 5).
- The area of triangle AEB can be calculated using the formula:
Area=12×base×height
- Here, base AB = 5 cm and height is the y-coordinate of point E, which is 5 cm.
- Thus, the area is:
Area=12×5×5=252 cm2.
The area of triangle AEB is 252 cm2.
Topper's Solved these Questions
- OLYMPIAD 2019-20BOOK - OSWAL PUBLICATIONCHAPTER - OLYMPIAD 2019-20EXERCISE - 8. Circles
1 Videos
- OLYMPIAD 2019-20BOOK - OSWAL PUBLICATIONCHAPTER - OLYMPIAD 2019-20EXERCISE - 10. Introduction to Trigonometry
1 Videos
- OLYMPIAD 2019-20BOOK - OSWAL PUBLICATIONCHAPTER - OLYMPIAD 2019-20EXERCISE - 5. Arithmetic Progressions
2 Videos
- NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Probability Stage -2
1 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - OSWAL PUBLICATIONCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Self- Assessment
14 Videos
Similar Questions
Knowledge Check
AB, EF and CD are parallel lines. Given that EG=5cm, GC= 10 cm, AB = 15 cm and DC= 18 cm. What is the value of AC?
 A20 cmB24 cmC25 cmD28 cm
A20 cmB24 cmC25 cmD28 cmABCD is a parallelogram with base AB = 12 cm and height 5 cm. If E and F are respectively midpoint of AB and CD and diagonal BD intersects AF and CE respectively at P and Q then area of quadrilateral PQCF is
A12 cm2B18 cm2C20 cm2D15 cm2ABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
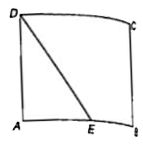 A400cm2B625cm2C729cm2D576cm2
A400cm2B625cm2C729cm2D576cm2
In a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View SolutionIn a trapezium ABCD, DC || AB , AB = 12 cm and DC = 7.2 cm. What is the length of the line segment joining the mid- points of its diagonals?
View SolutionB is a point on line segment AC such that AB: BC is 3 : 2. If AC = 40 cm, then length of BC is
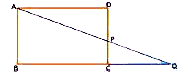
View SolutionIn the given figure,ABCD is a rectangle and P is a point on DC such that BC=24 cm, DP = 10 cm, and CD=15 cm .If AP produced intersect BC produced at Q. then find the length of AQ.
View Solution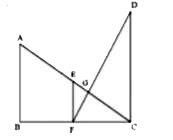
AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC?
View Solution
