In the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
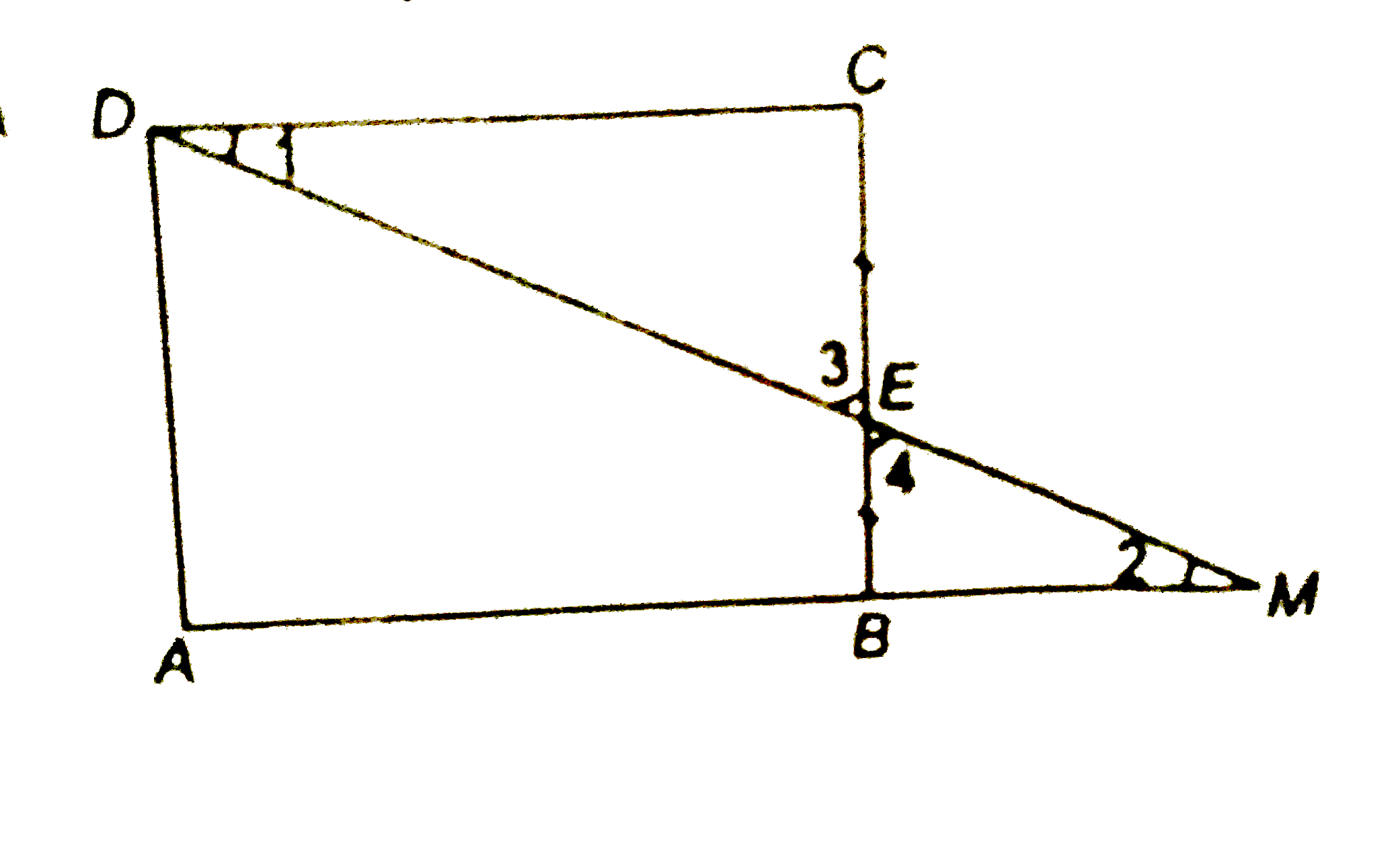
(i) Since ABCD is a parallelogram
∴ABM||DC
∴∠1=∠2 (alternate angles)
Now, in ΔDCE and ΔMBE
∴⎧⎪⎨⎪⎩∠1=∠2(proved above)∠3=∠4(vertically opposite angles)CE=BE(given as E is the mid-point)
∴ΔDCE≅ΔMBE (AAS) Hence Proved.
(ii) Therefore, DC=MB (c.p.c.t.)
But DC=AB (opposite sides of a parallelogram are equal)
∴AB=MB Hence Proved.
(iii) Now, AM=AB+BM
=DC+DC (poved above)
=2DC Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
From the given diagram, in which ABCD is a parallelgram, ABL is a line segment and E is mid point of BC. Prove that :
(i) ΔDCE≅ΔLBE
(ii) AB = BL
(iii) AL = 2DC
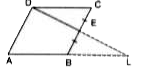
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
ΔDCE≅ΔLBE

View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AL=2DC
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AB=BL
View SolutionABCD is a parallelogram. If AB = 2AD and P is the mid-point of CD, prove that ∠APB=90∘
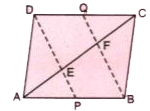
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that AE=EF=FC.
View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
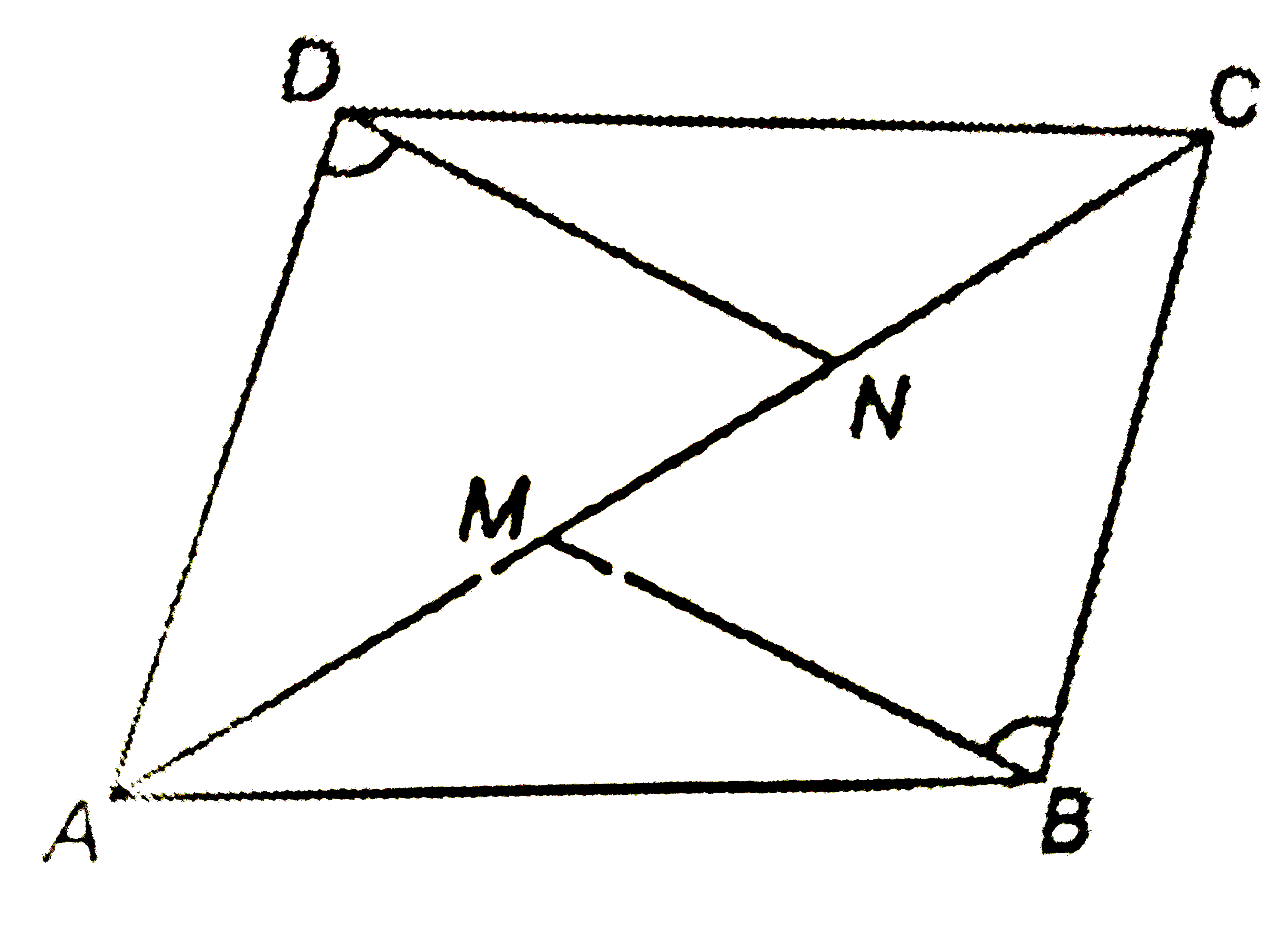
View SolutionIn the adjoining figure, ABCD is a parallelogram. If ∠MBC=∠NDA, prove that AM=NC.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View Solution
