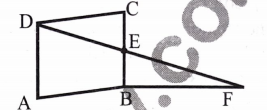
In the adjoining figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
△DEC=△FEB,So,BF=DC=AB.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C
18 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
47 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2
In the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionIn the given figure, ABCD is a quadrilateral in which AB∣∣DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB=CQ, (ii) DQ=DC+AB
View SolutionIn the given figure ABCD is a quadrilateral in which AB||DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i)AB=CQ,(ii)DQ=DC+AB.

View SolutionIn ΔABC, E is the midpoint of the median AD. BE produced meets AC at F. Prove that AF=(13)AC
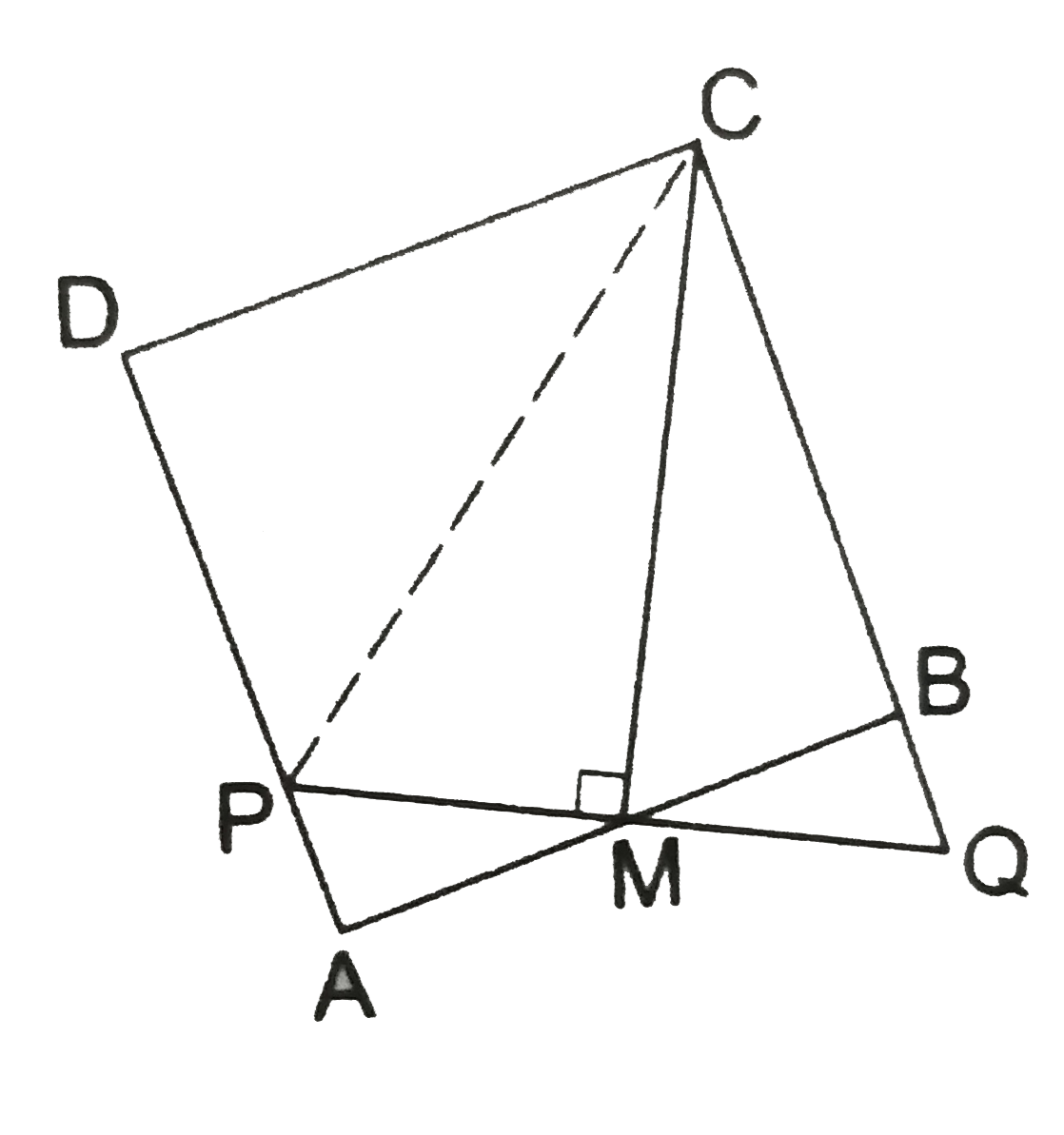
View SolutionIn the given figure, ABCD is a square, M is the midpoint of AB and PQ⊥CM meets AD at P and CB produced at Q. Prove that (i) PA = QB and (ii) CP=AB+PA.
View Solution