In the adjoining figure, ABCD is a parallelogram whose diagonals intersect each other at O. A line segment EOF is drawn to meet AB at E and DC at F. Prove that OE = OF.
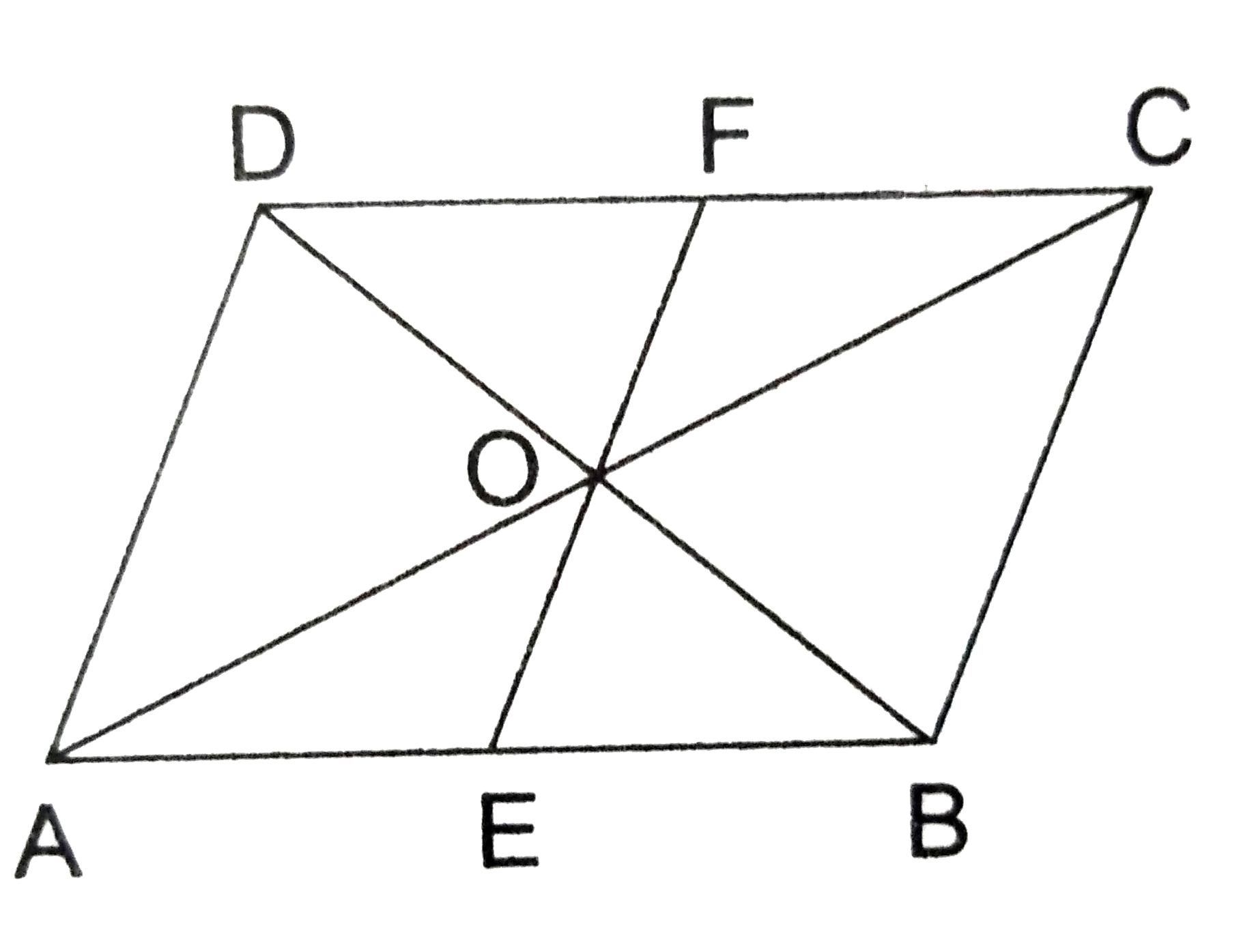
△ODF≅△OBE(∵OD=OB,∠DOF=∠BOEand∠ODF=∠OBE).
∴OF=OE.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C
18 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
47 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar (ΔPOA)= ar (ΔQOC).
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution
Knowledge Check
Let ABCD be a parallelogram whose diagonals intersect at P and O be the origin, then OA+OB+OC+OD equals
AOPB2OPC3OPD4OPIn the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
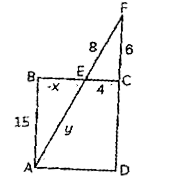
Perimeter of ΔABE=A35cmB36cmC40cmD45cm
The diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
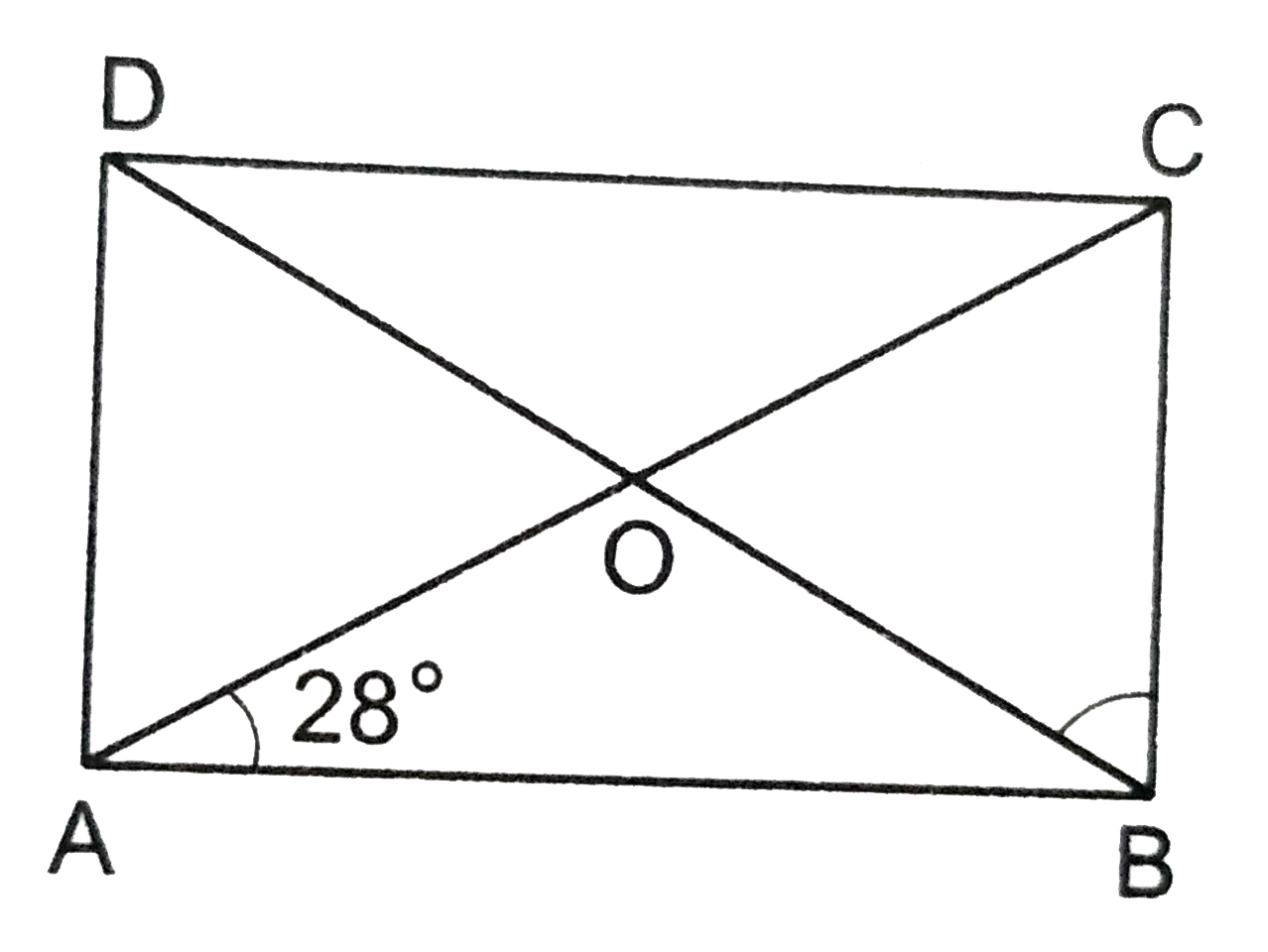
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
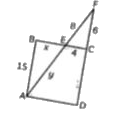
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View SolutionIn a parallelogram ABCD, prove that it is a rhombus, if diagonals bisect each other at 90∘
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect each other at point O. If ∠CAB=25∘ and ∠BCD=85∘ then find ∠CBD.
View Solution
