In the adjoining figure, AD is a median of △ABC and E is the midpoint of AD. Also, BE produced meets AC in F. Prove that AF=13AC.
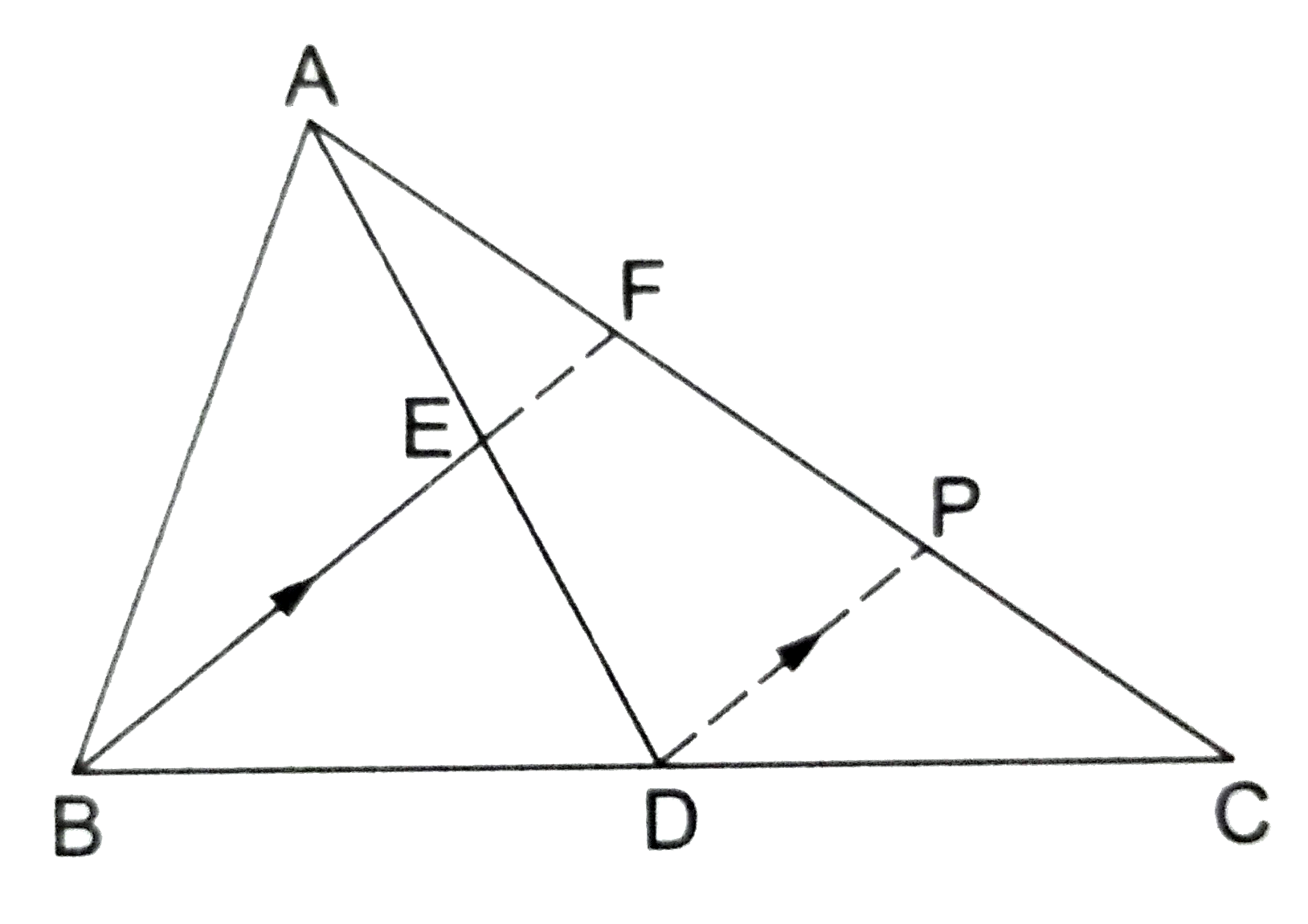
Draw DP||EF.
In △ADP, E is the midpoint of AD and EF||DP.
∴ F is the midpoint of AP, i.e., AF = FP.
In △FBC, D is the midpoint of BC and DP||BF. ltbr> ∴ P is the midpoint of FC, i.e., FP = PC.
Thus, AF = FP = PC.
Hence, AF = 13AC.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
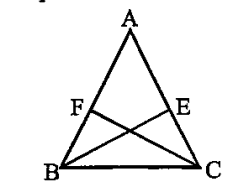 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
In a triangle ABC, AD is the median through A and E is the midpoint of AD, and BE produced meets AC at F. Then AF is equal to
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
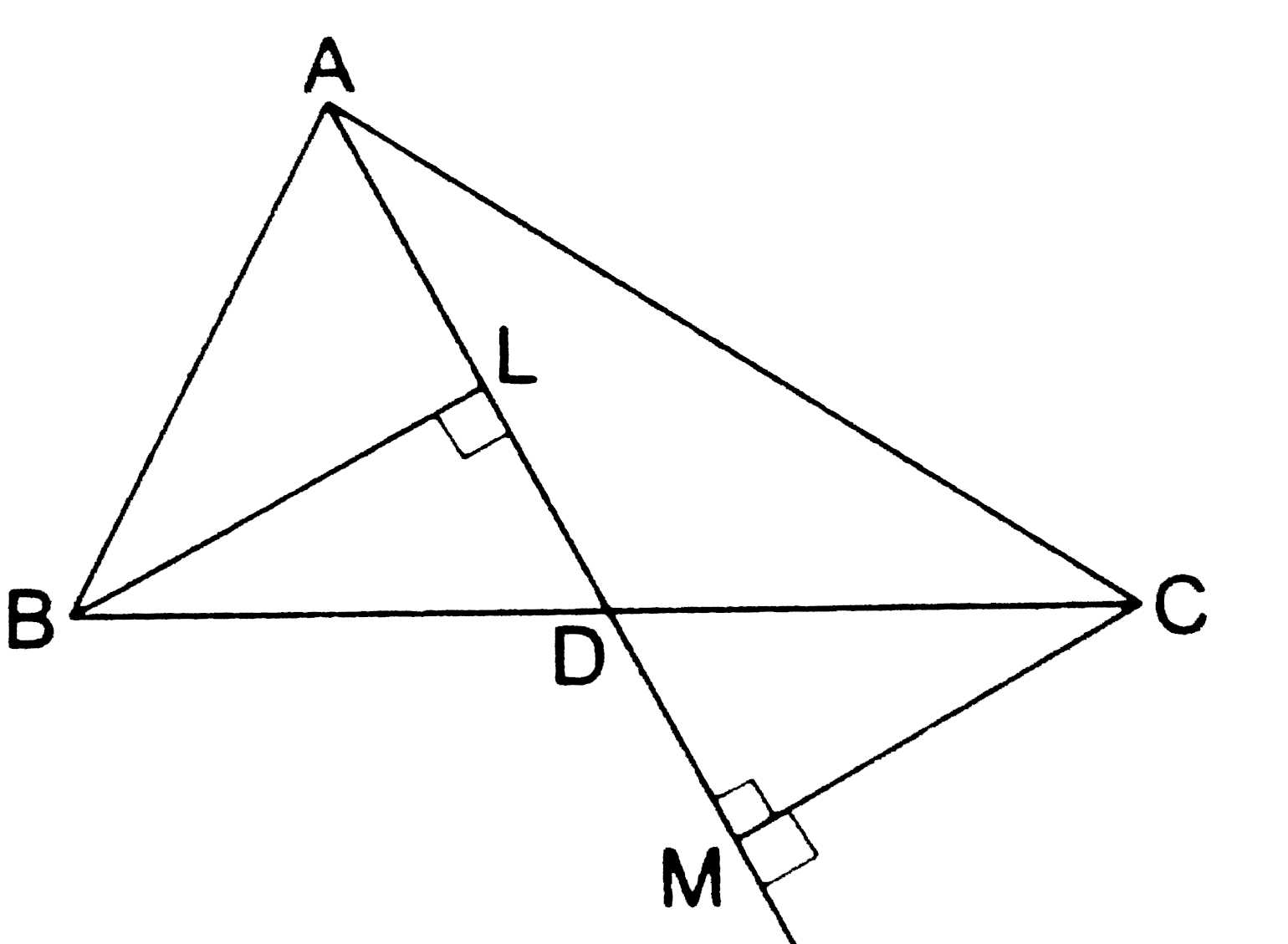
View SolutionIn the adjoining figure, AD is a median of ΔABC. If BL and CM are drawn perpendiculars on AD and AD produced, prove that BL = CM.
View SolutionIn the adjoining figure, if AD is the bisector of ∠A , what is AC ?
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View Solution
