In the adjoining figure, P is an interior point of ΔABC. Then prove that :
AB+BC+CA<2(PA+PB+PC)

Step by step video & image solution for In the adjoining figure, P is an interior point of DeltaABC. Then prove that : AB+BC+CA lt 2(PA + PB +PC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Let O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionP is any point in the interior of a triangle ABC.
Prove that : PA+PB<AC+BC
View SolutionP is any point in the interior of a triangle ABC.
Prove that : PA+PB<AC+BC
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
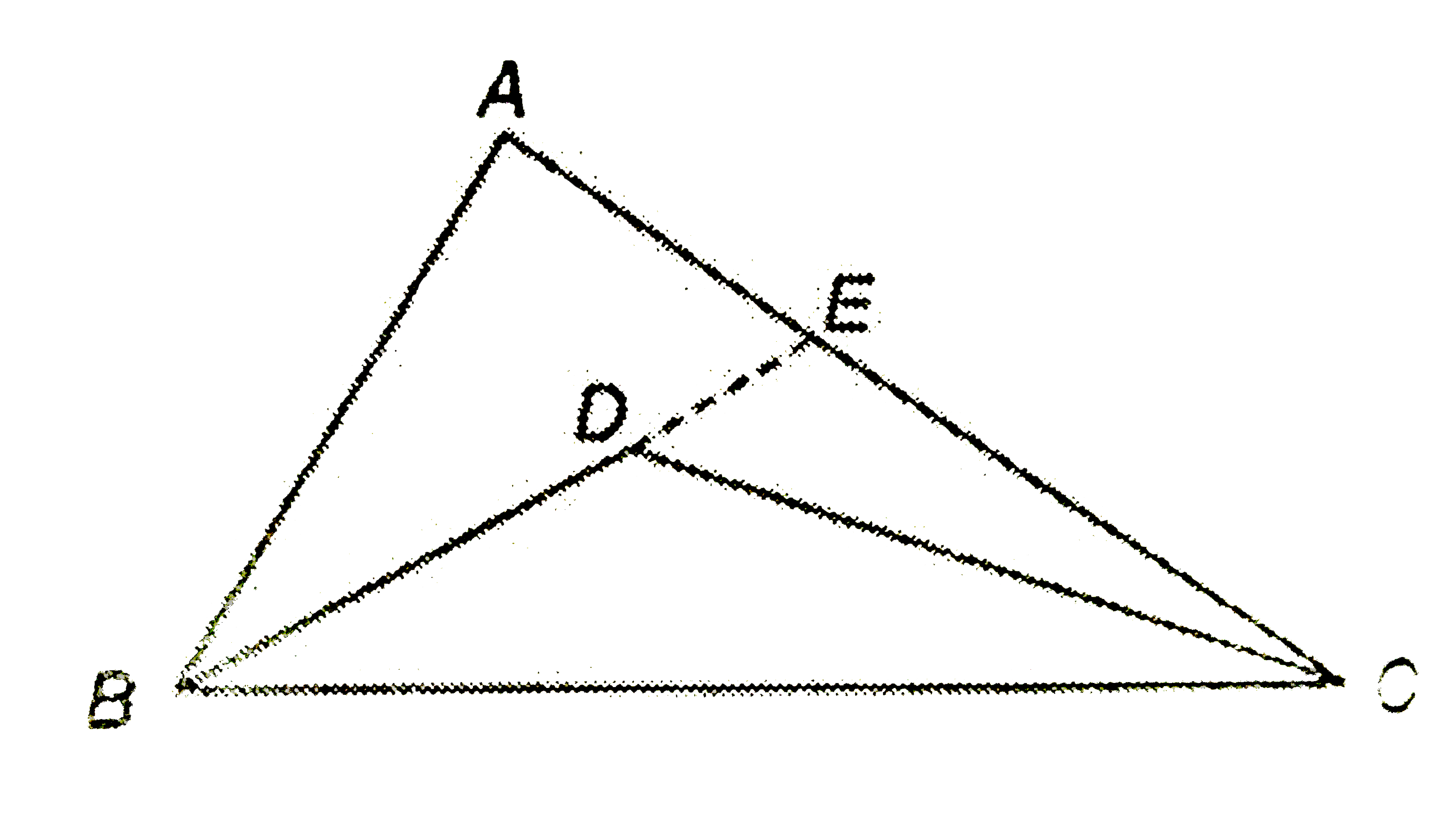
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View SolutionIn the adjoining figure, if AB = BC and BX =BY, then show that AX=CY
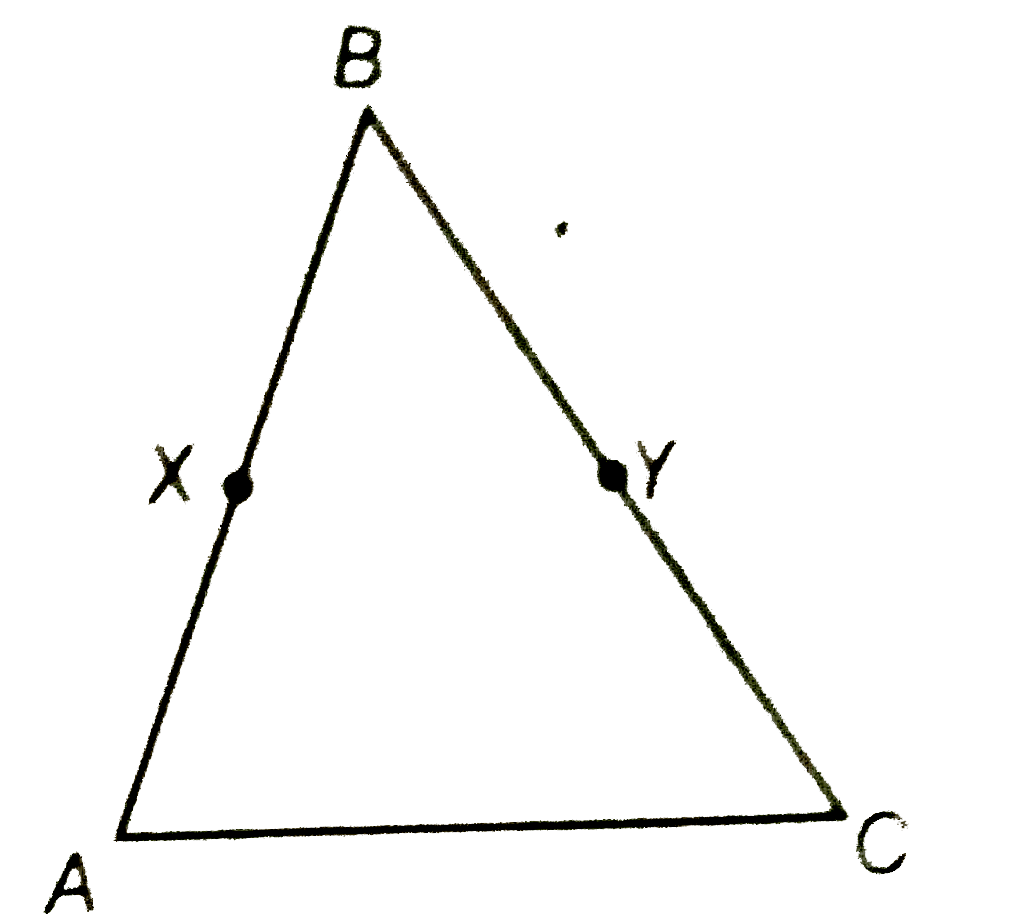
View SolutionIn the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)

View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC
View Solution
