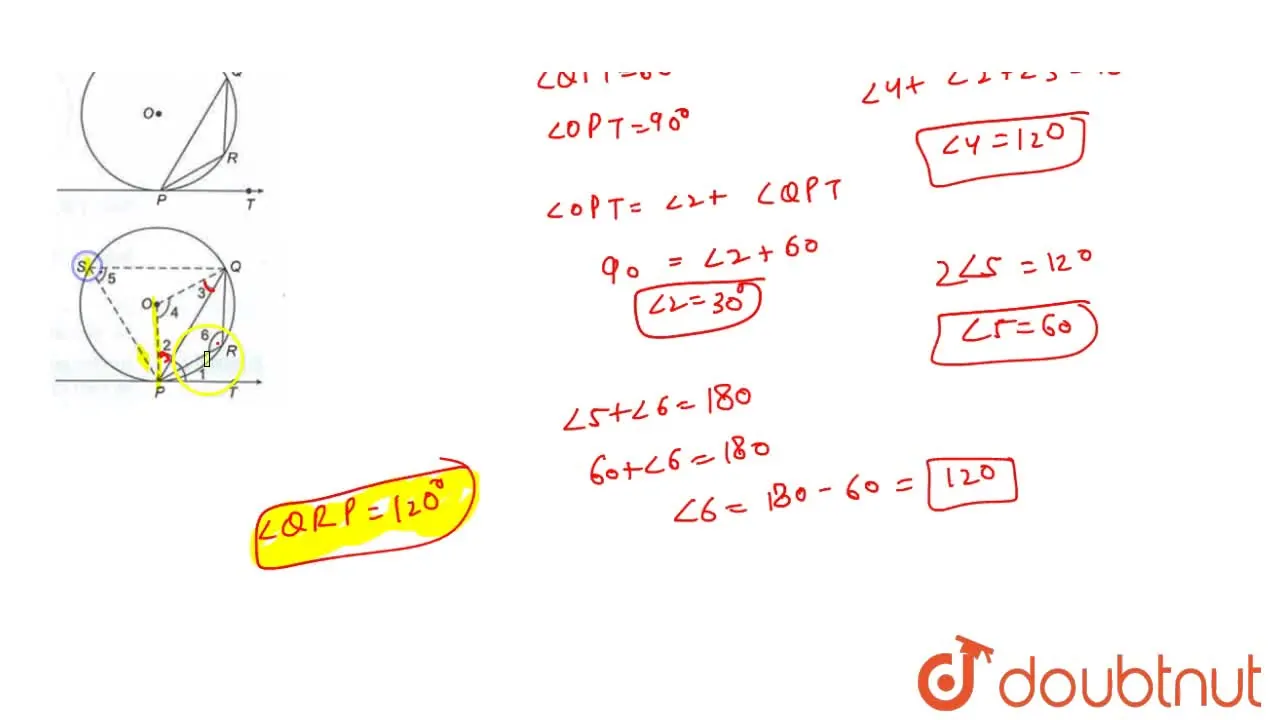
In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
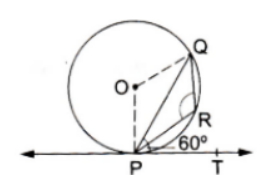
Join OP and OQ. Take any point S on the circumference in the alternate segment. Join SP and SQ.
Since, OP⊥PT
(radius through point of contact is bot to the tangent)

∴ ∠2+∠1=90∘
⇒ ∠2+60∘=90∘ (given)
⇒ ∠2=90∘−60∘=30∘ ...(1)
But OP=OQ (each radii)
∴ ∠2=∠3(angles opposite to equal sides are equal)
...(2)
Now in ΔPOQ,
∠2+∠3+∠4=180∘ (angle sum property)
⇒30∘+30∘+∠4=180∘ [from(1)and(2)]
⇒ ∠4=120∘
∴ ∠5=12×∠4
(∵ degree measure of an are is twice the angle subtended by it in alternate segment)
⇒ ∠5=12×120∘
⇒ ∠5−60∘
Also, ∠5+∠6=180∘ (Sum of opposit angles of a cyclic quad.)
⇒ 60∘+∠6=180∘
⇒ ∠6=∠PRQ=120∘
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar11videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
 View Solution
View SolutionIn the adjoining figure PQ||RS find x and y.
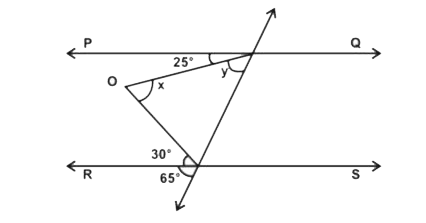 View Solution
View SolutionPQ is a chord of a circle with centre O and PT is the tangent at P such that ∠QPT=70∘. Then the measure of ∠PRQ is equal to :
(A) 135∘ (B) 150∘ (C) 120∘ (D) 110∘View SolutionIn the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
View SolutionIn Figure PQ is a chord of a circle with centre O and PT is a tangent. If QPT=60∘ so, find PRQ.
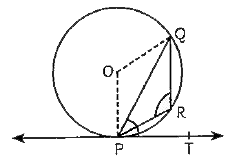 View Solution
View SolutionIn the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. ∠BDQ=48∘. Find the ratio of angleDBA:angleDCB.
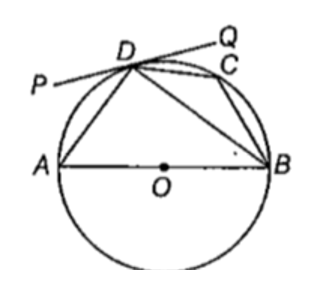 View Solution
View SolutionIn Fig , O is the centre of a circle , PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ. Find ∠POQ .
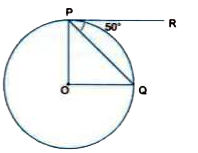 View Solution
View SolutionIn the adjoining figure 'O' is the centre of the circle and PQ, PR and ST are the three tangents. ∠QPR=50∘, then the value of ∠SOT is :
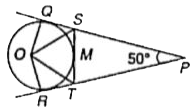 View Solution
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 View Solution
View SolutionIn the adjoining figure , Q is the centre of the circle and PM,PN are tangent segments to the circle. IF ∠MPN=40∘ , find ∠MQN.
 View Solution
View Solution