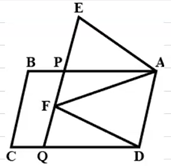
In the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
Step by step video & image solution for In the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(DeltaADE) = ar(DeltaBCF). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Multiple Choice Questions )45videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )2videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.3)19videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER6videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
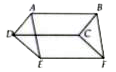
In the given figure, ABCD and AEFD a re two parallelograms.
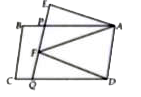
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB) - Question 2 - Select One
In the given figure, ABCD and AEFD a re two parallelograms.
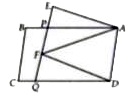
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these - Question 3 - Select One
In the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
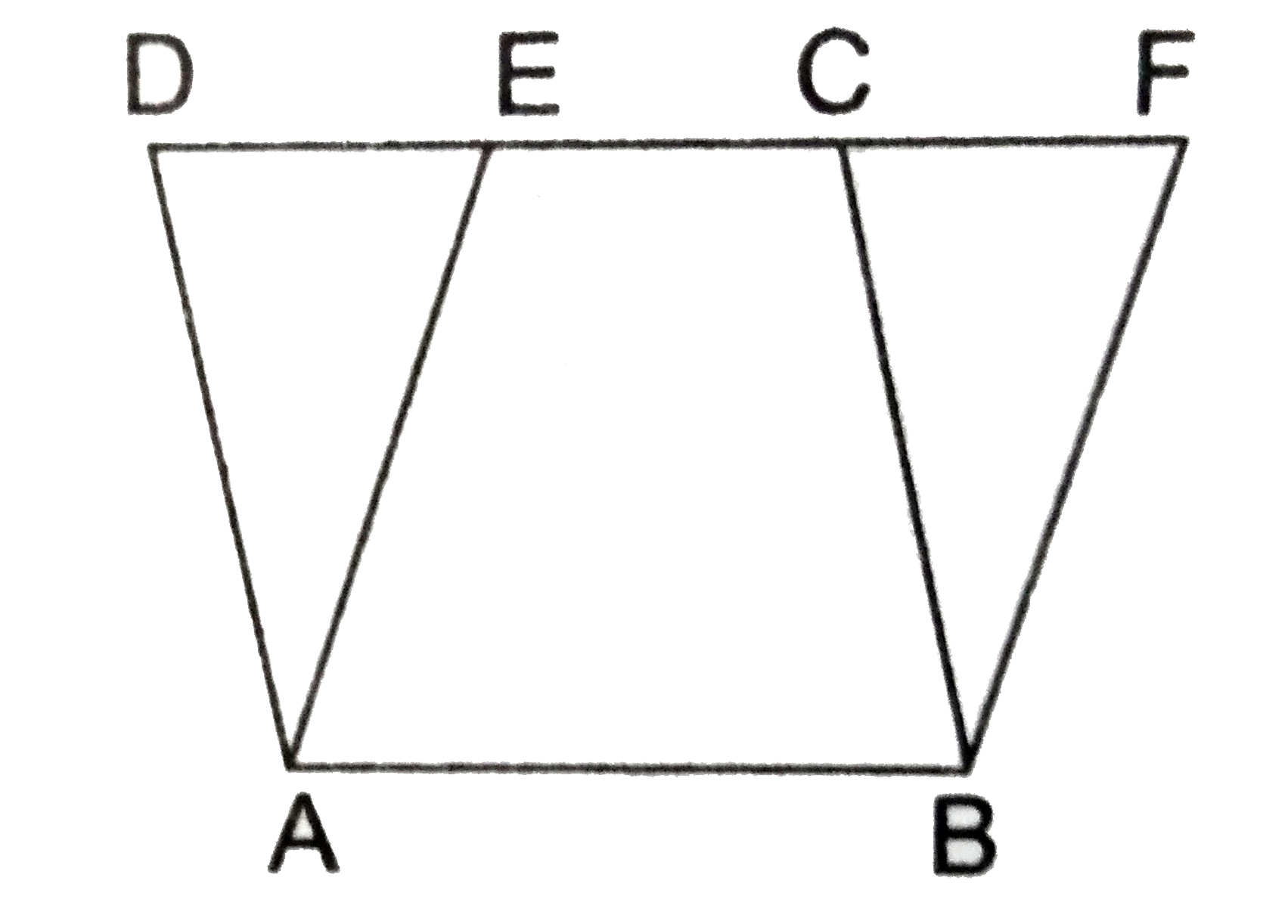 A4cm2B4.8cm2C6cm2D8cm2
A4cm2B4.8cm2C6cm2D8cm2
In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
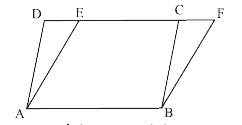
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
 View Solution
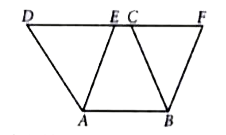
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
 View Solution
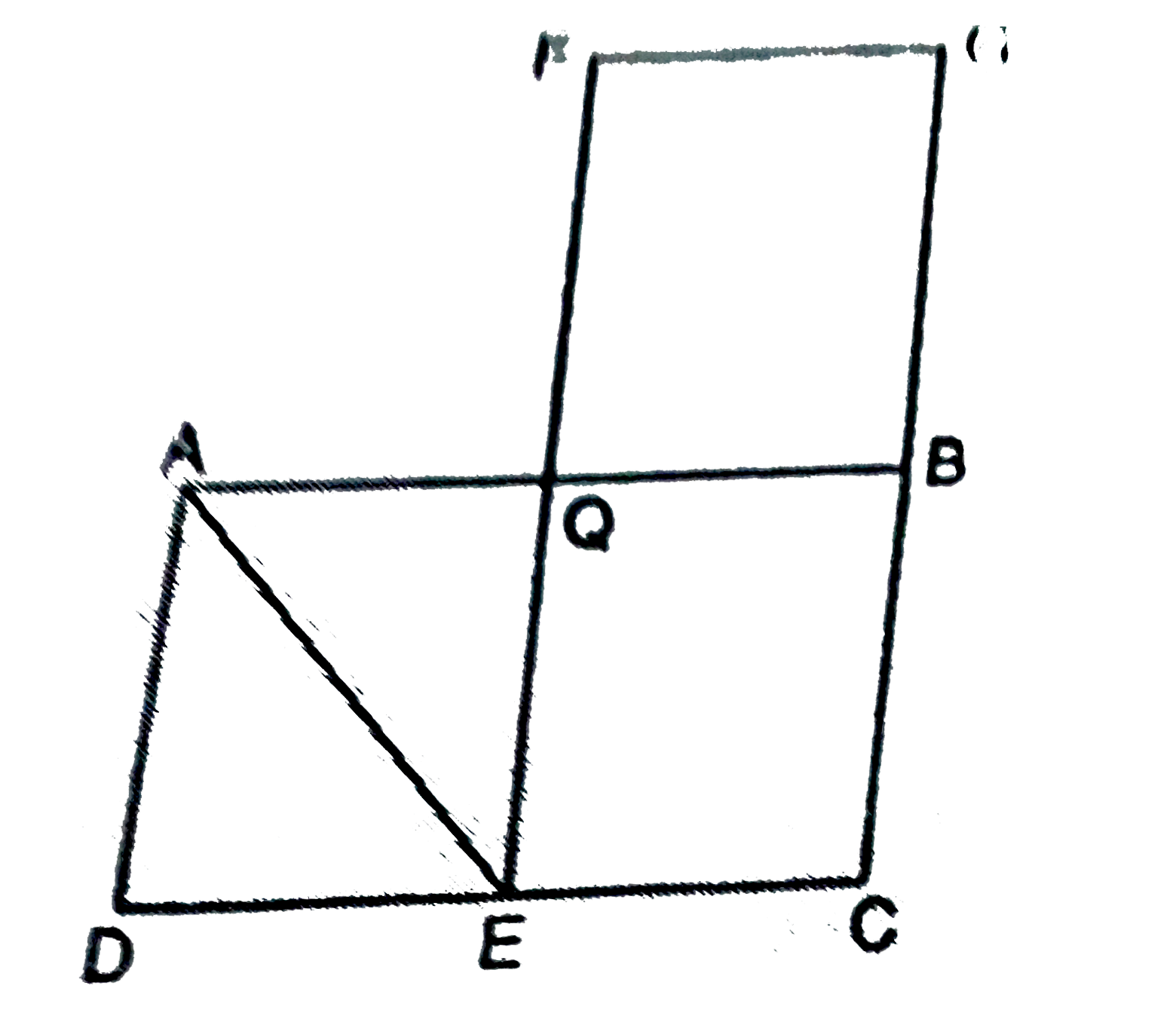
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
 View Solution
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that ar (APB) = ar (BQC).
View Solution