In the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
To prove that point P is equidistant from points A and B, we will use the properties of triangles and the concept of congruence.
1. Identify the Given Information:
- BX bisects angle ABC.
- CY is perpendicular to AB.
- Y is the midpoint of AB.
- P is the intersection of BX and CY.
2. Draw Right Triangles:
- Consider triangles PAY and PBY.
- Since CY is perpendicular to AB, angles PYA and PYB are both right angles (90 degrees).
3. Establish Common Sides:
- In triangles PAY and PBY, the segment PY is common to both triangles.
4. Use the Midpoint Property:
- Since Y is the midpoint of AB, we have AY = BY.
5. Apply the Criteria for Congruence:
- Now we have:
- Angle PYA = Angle PYB (both are 90 degrees)
- PY = PY (common side)
- AY = BY (since Y is the midpoint)
- By the criteria of congruence (RHS - Right angle, Hypotenuse, Side), we can conclude that triangle PAY is congruent to triangle PBY.
6. Conclude the Distances:
- Since the triangles are congruent, we can say that PA = PB.
- Therefore, point P is equidistant from points A and B.
Final Statement:
Thus, we have proved that point P is equidistant from points A and B.
---
- BX bisects angle ABC.
- CY is perpendicular to AB.
- Y is the midpoint of AB.
- P is the intersection of BX and CY.
- Consider triangles PAY and PBY.
- Since CY is perpendicular to AB, angles PYA and PYB are both right angles (90 degrees).
- In triangles PAY and PBY, the segment PY is common to both triangles.
- Since Y is the midpoint of AB, we have AY = BY.
- Now we have:
- Angle PYA = Angle PYB (both are 90 degrees)
- PY = PY (common side)
- AY = BY (since Y is the midpoint)
- By the criteria of congruence (RHS - Right angle, Hypotenuse, Side), we can conclude that triangle PAY is congruent to triangle PBY.
- Since the triangles are congruent, we can say that PA = PB.
- Therefore, point P is equidistant from points A and B.
Thus, we have proved that point P is equidistant from points A and B.
Topper's Solved these Questions
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(A)
26 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
- MATHEMATICS -2014BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B
29 Videos
Similar Questions
In the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
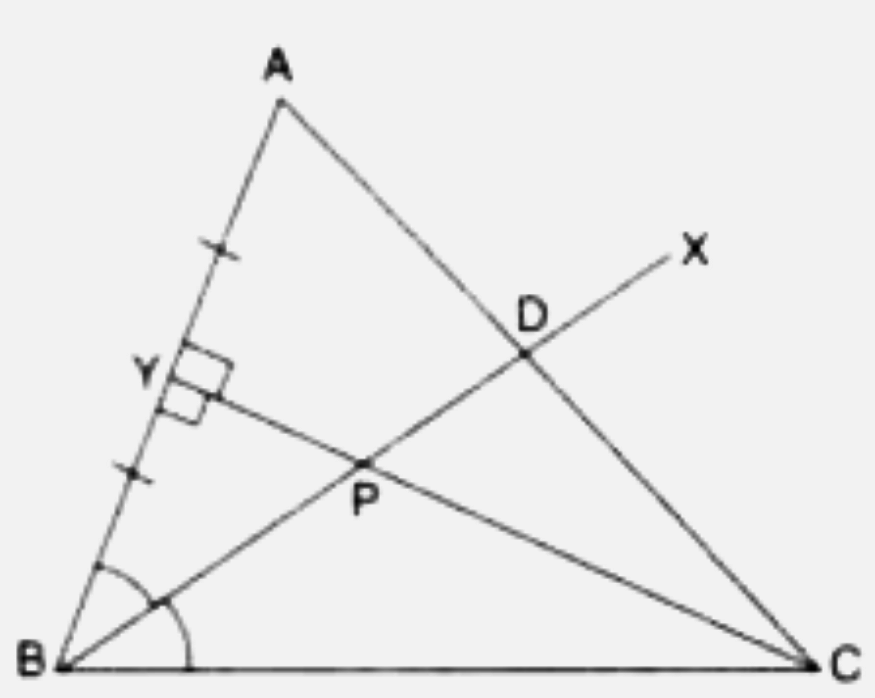
point D is equidistant from AB and BC.
View SolutionAB is a given line segment with a point C on it . Draw a line segment perpendicular to AB at the point C.
View Solution
Knowledge Check
If a certain line intersects the origin and is perpendicular to the line with the equation y=2x+5 at point P, what is the distance from the origin to point P ?
A2.24B2.45C2.67D3.25
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and B
View SolutionIf AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
View SolutionDraw a perpendicular to a given line segment AB though a point P lying outside AB.
View SolutionDraw a line segment AB = 6 cm. Take a point P above this line segment. Draw a perpendicular to AB through the point P.
View SolutionIn ΔABC,AB=AC and the bisectors of angles B and C intersect at point O. Prove that
BO=OC
View Solution
