In the given figure, ABCD is a square and ∠PQR=90∘. If PB=QC=DR, prove that
(i) QB=RC, (ii) PQ=QR, (iii) ∠QPR=45∘.
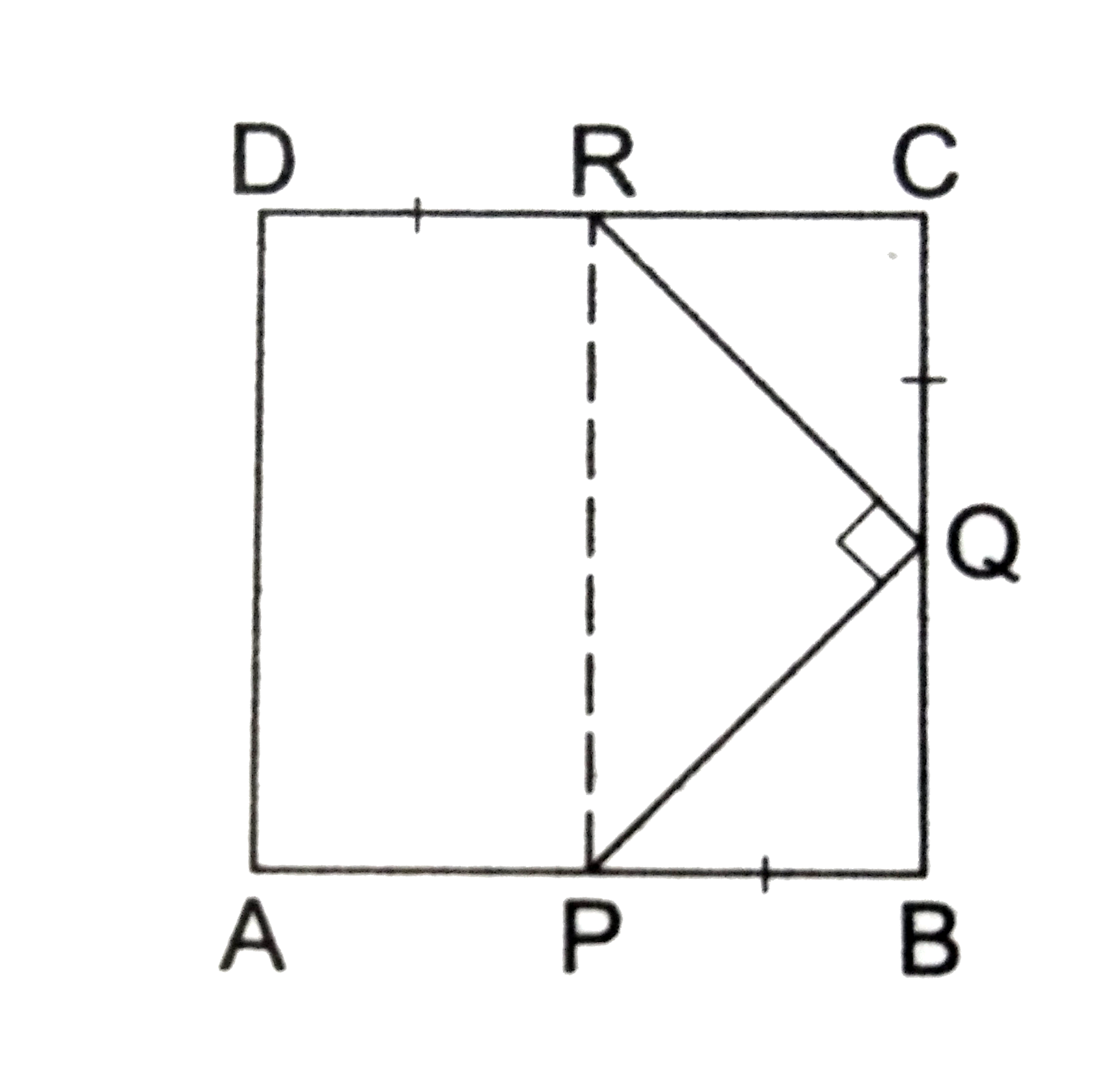
BC=DC,CQ=DR⇒BC−CQ=DC−DR⇒QB=RC.
From △CQR,∠RQB=∠QCR+∠QRC
⇒∠RQP+∠PQB=90∘+∠QRC
⇒90∘+∠PQB=90∘+∠QRC⇒∠PQB=∠QRC.
Now, △RCQ≅△QBP and therefore , QR=PQ.
PQ=QR⇒∠QPR=∠PRQ.
But, ∠QPR+∠PRQ=90∘. So, ∠QPR=45∘.
Similar Questions
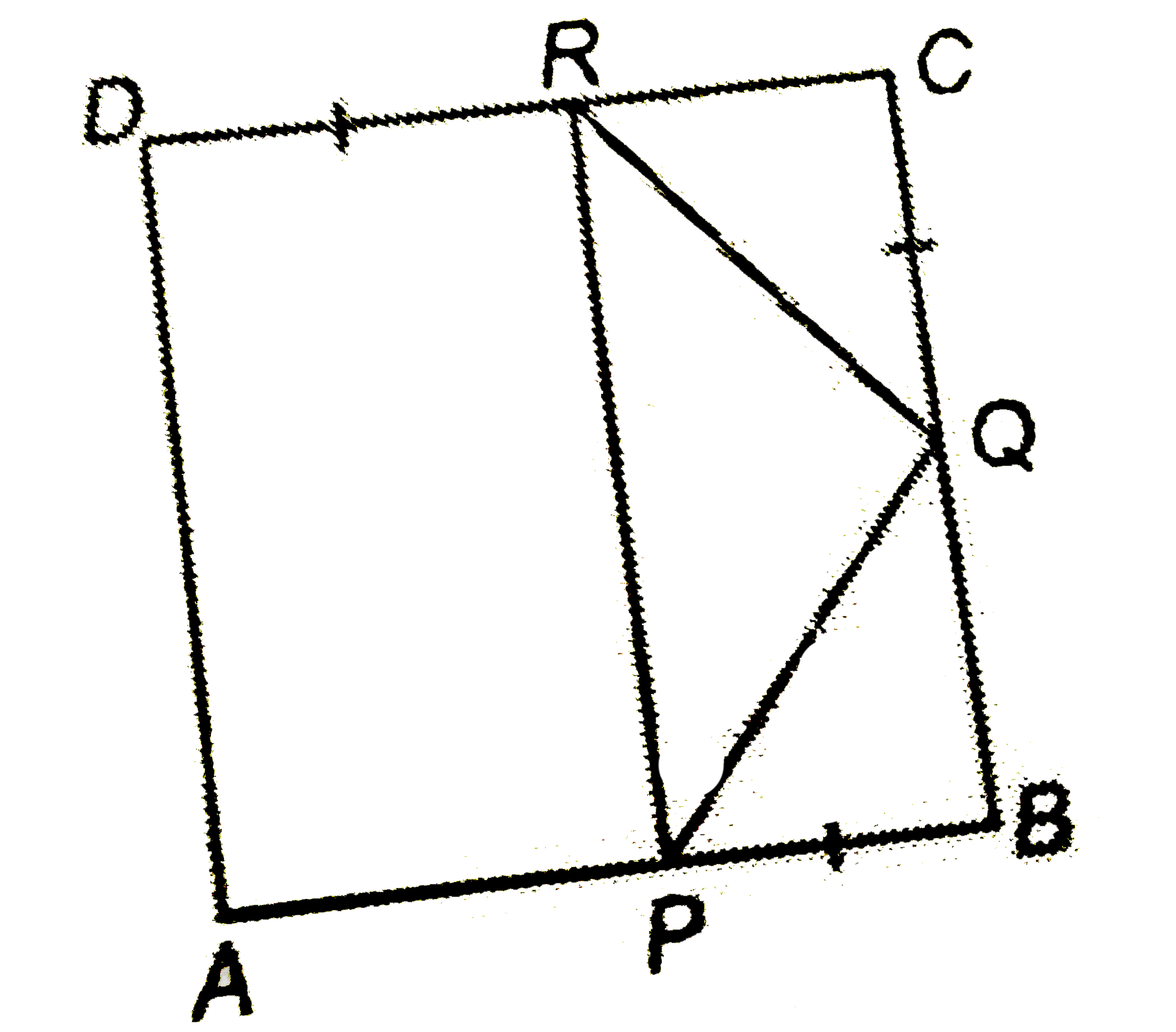
In the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
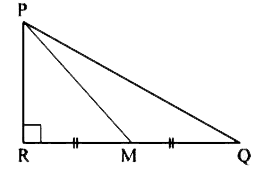
View SolutionIn the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
View SolutionIn the given figure, DEFG is a square and ∠BAC=90∘, Prove that
(i)ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii)DE2=BD×EC

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D

View SolutionIn the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.

View SolutionIn the given figure, ABCD is a square and P is a point inside it such that PB=PD. Prove that CPA is a straight line.
View SolutionIn the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
View SolutionIn the given figure, ∠PQR=90∘, seg QN⊥segPR,PN=9,NR=16.Find QN.
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.

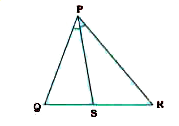
View SolutionIn the given figure, PR > PQ and PS bisects ∠ QPR. Prove that ∠PSR>∠PSQ.
View Solution
