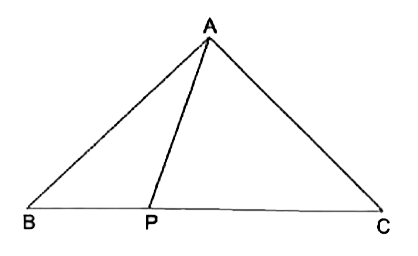
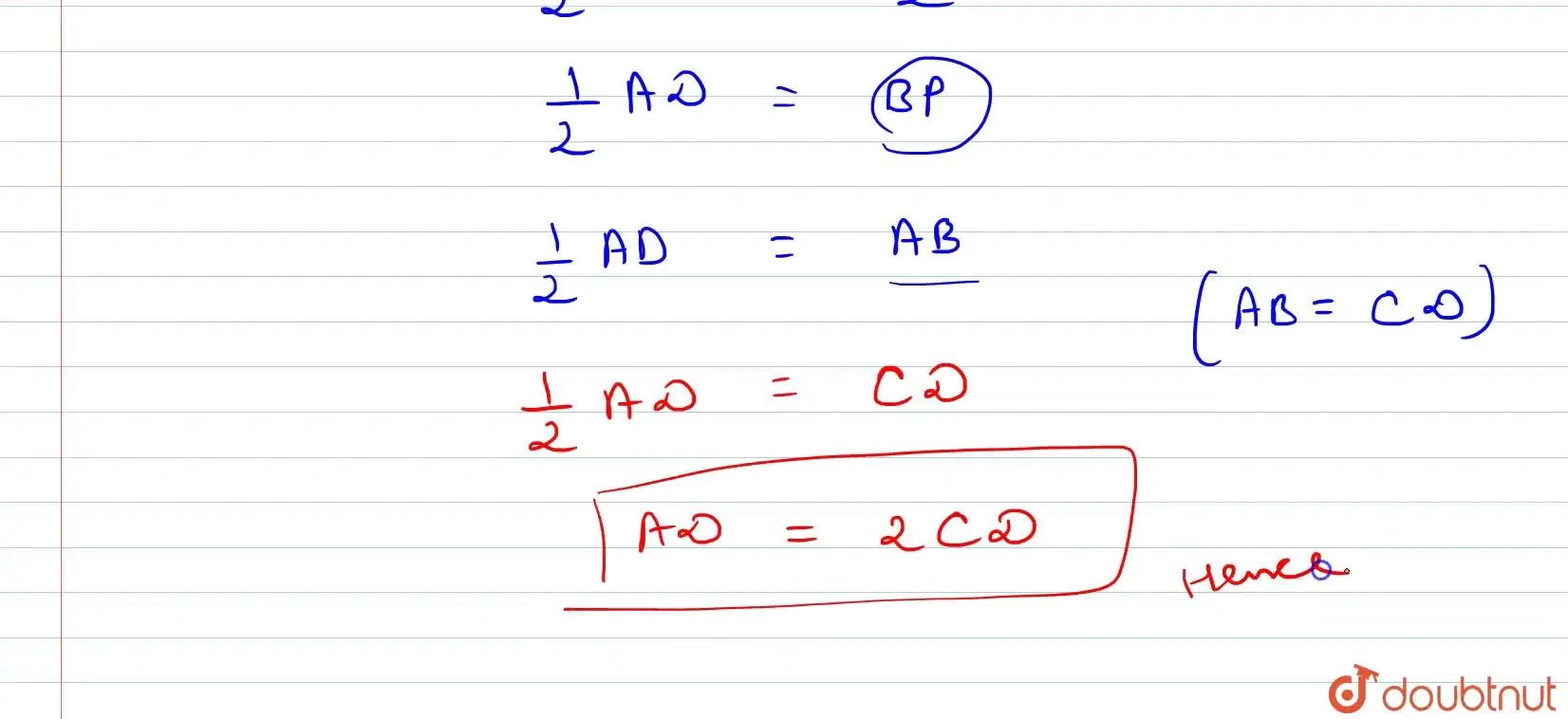In the given figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
∠BAP=∠DAP=12∠A …(1)
Since, ABCD is a parallelogram, we have
∠DAB+∠ABC=180∘ ..(2)
(∵sum of co-interior angles on the same side of transversal is180∘)
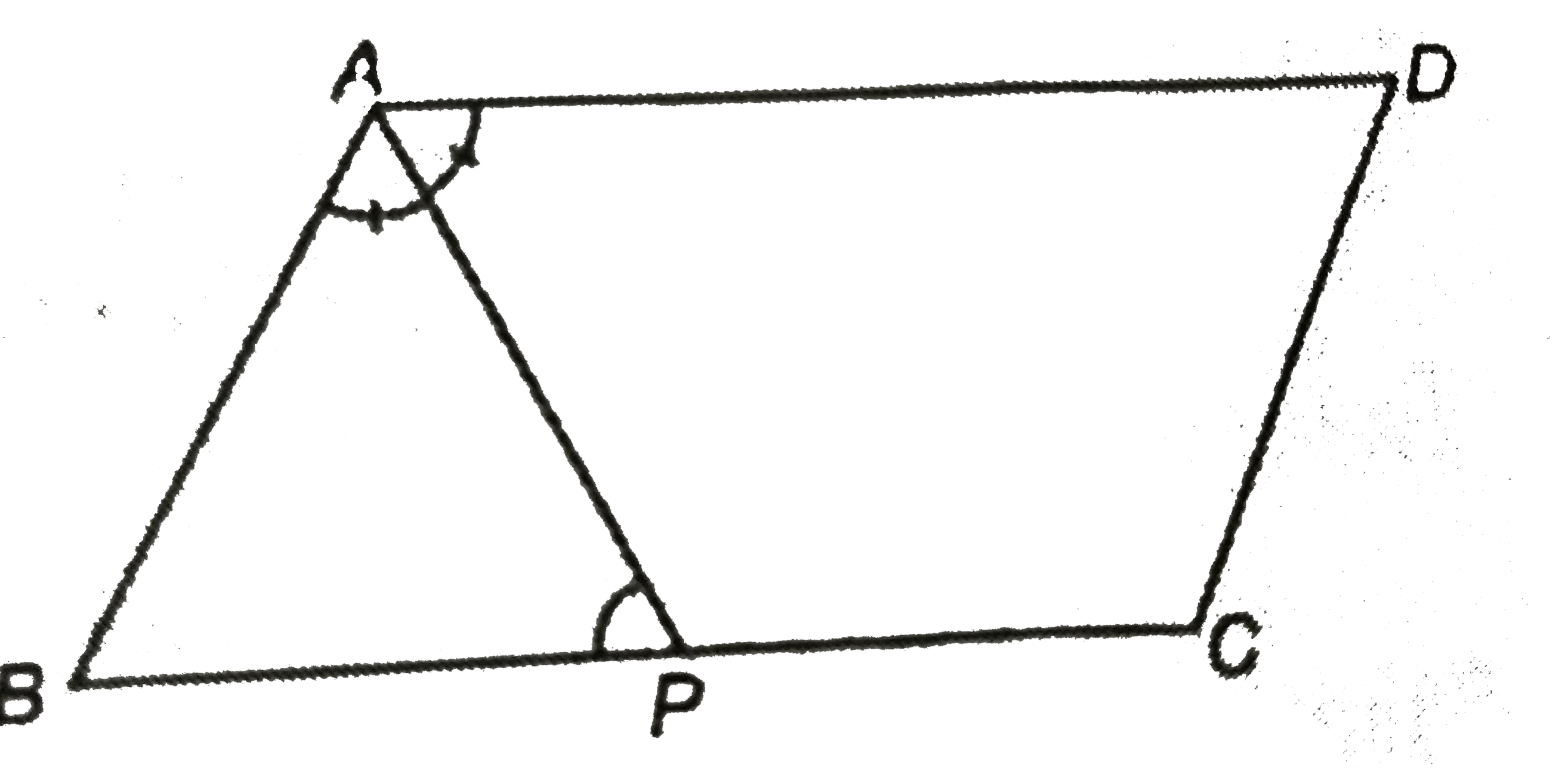
In ΔABP we have
∠BAP+∠B+∠APB=180∘ (angle sum property)
⇒12∠BAD+180∘−∠A+∠APB=180∘
⇒ ∠APB−12∠A [using (1) and (2)]
From (1) and (3), we get ...(3)
∠BAP=∠APB
BP=AB(∴side opposite to equal angles are equal)...(4)
Since, opposite sides of a parallelogram are equal, we have
AD=BC⇒12AD=12BC
⇒ 12AD=BP (∵Pis the mid-point of BC)
⇒ 12AD=AB [∵from(4)]
Since, opposite sides of a parallelogram are equal, we have
12AD=CD⇒AD=2CD
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)5videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
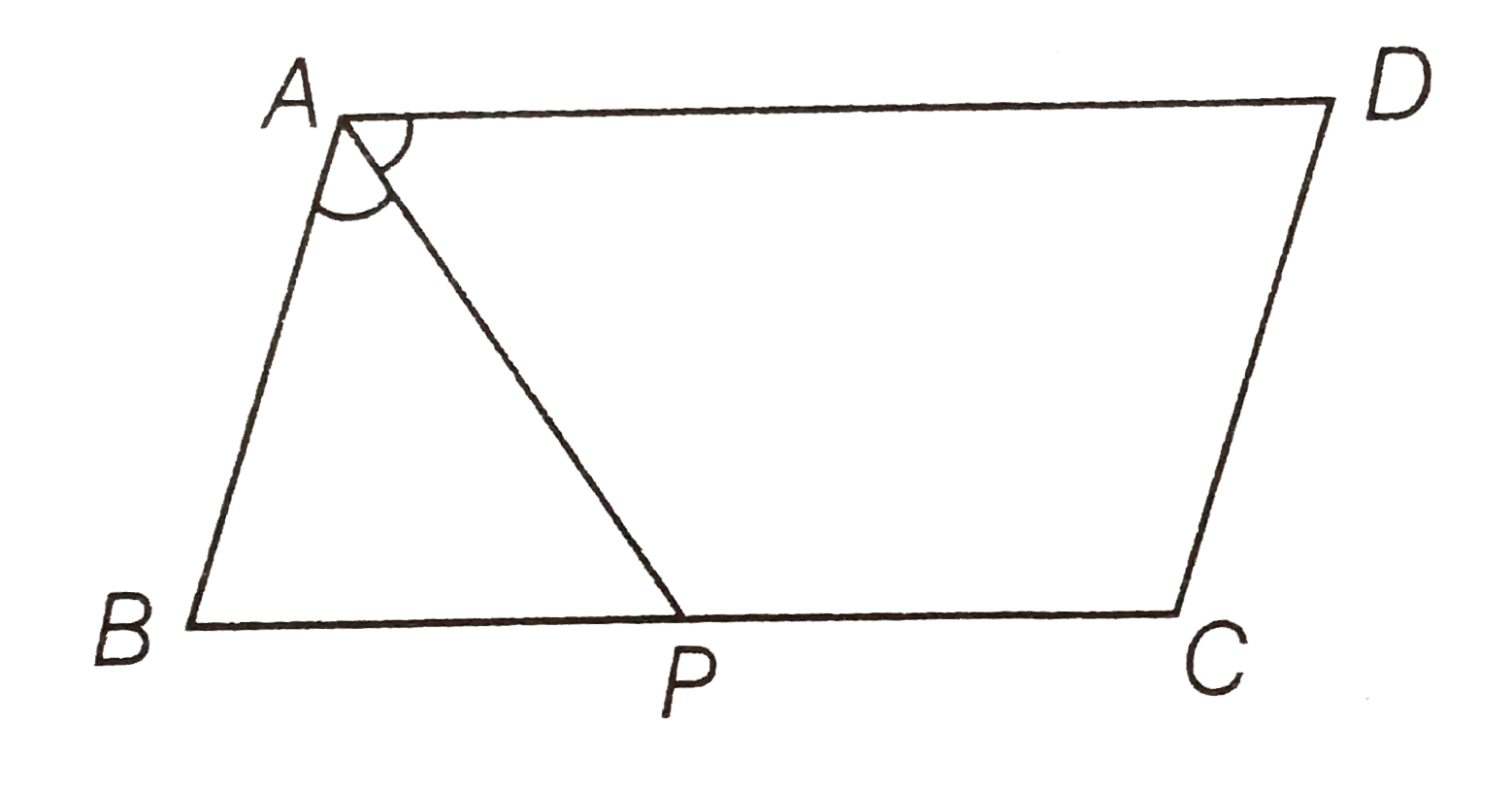
In figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD. ltBrgt
 View Solution
View SolutionIn the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?
 View Solution
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
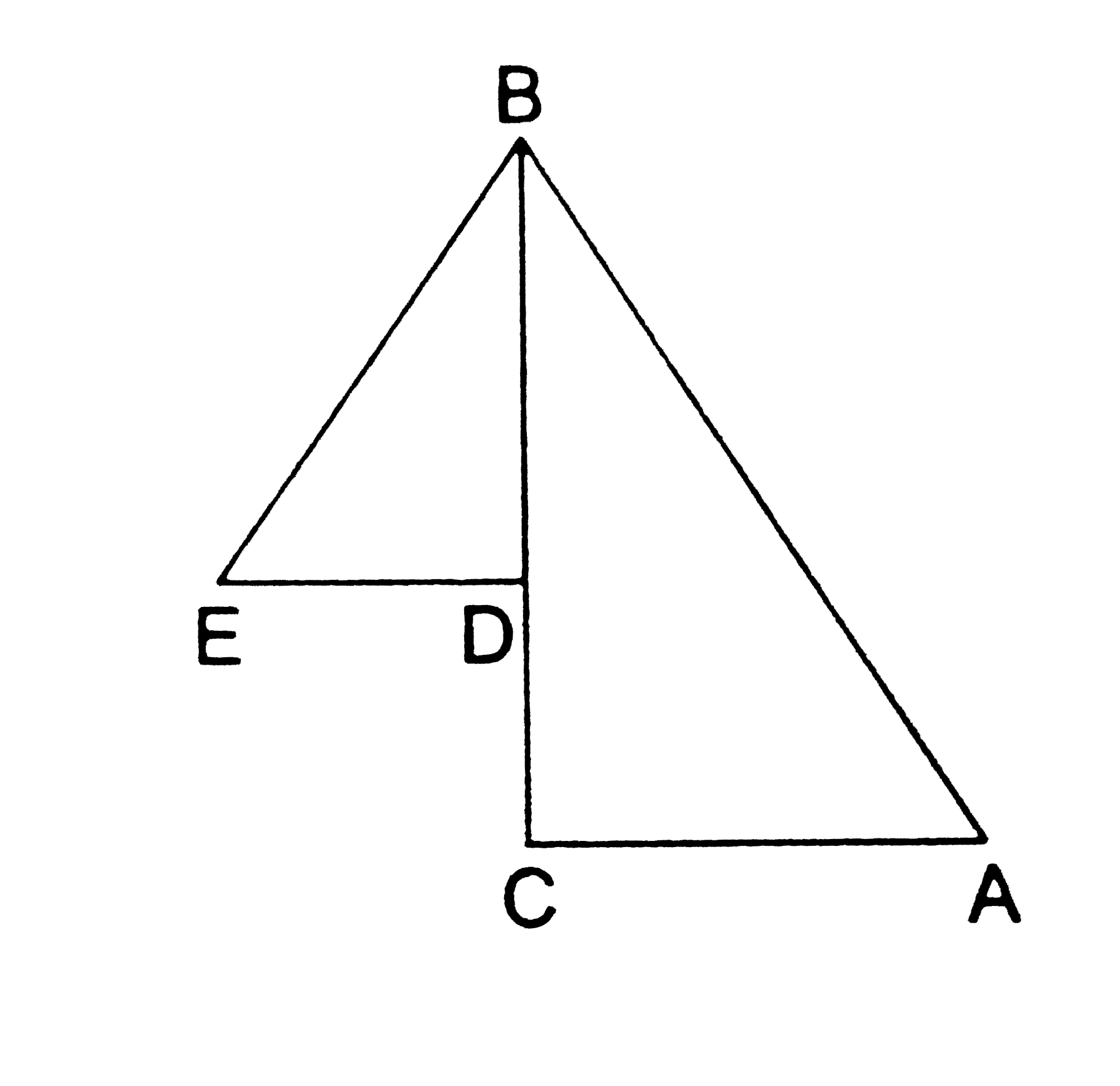 View Solution
View Solution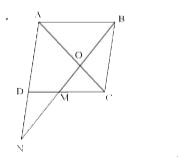
The mid-point of side CD of parallelogram ABCD is 'm' in the given figure what is the ratio ON : OB?View SolutionIn the given figure ,P is a point on the side BC of △ABC.Prove tat (AB+BC+AC)GT2AP
 View Solution
View SolutionIf D is the mid-point of the side BC of a triangle ABC, prove that →AB+→AC=2→AD.
View SolutionIn parallelogram ABCD, if P is the mid-point of side AB, then
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE~DCFB .
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View Solution