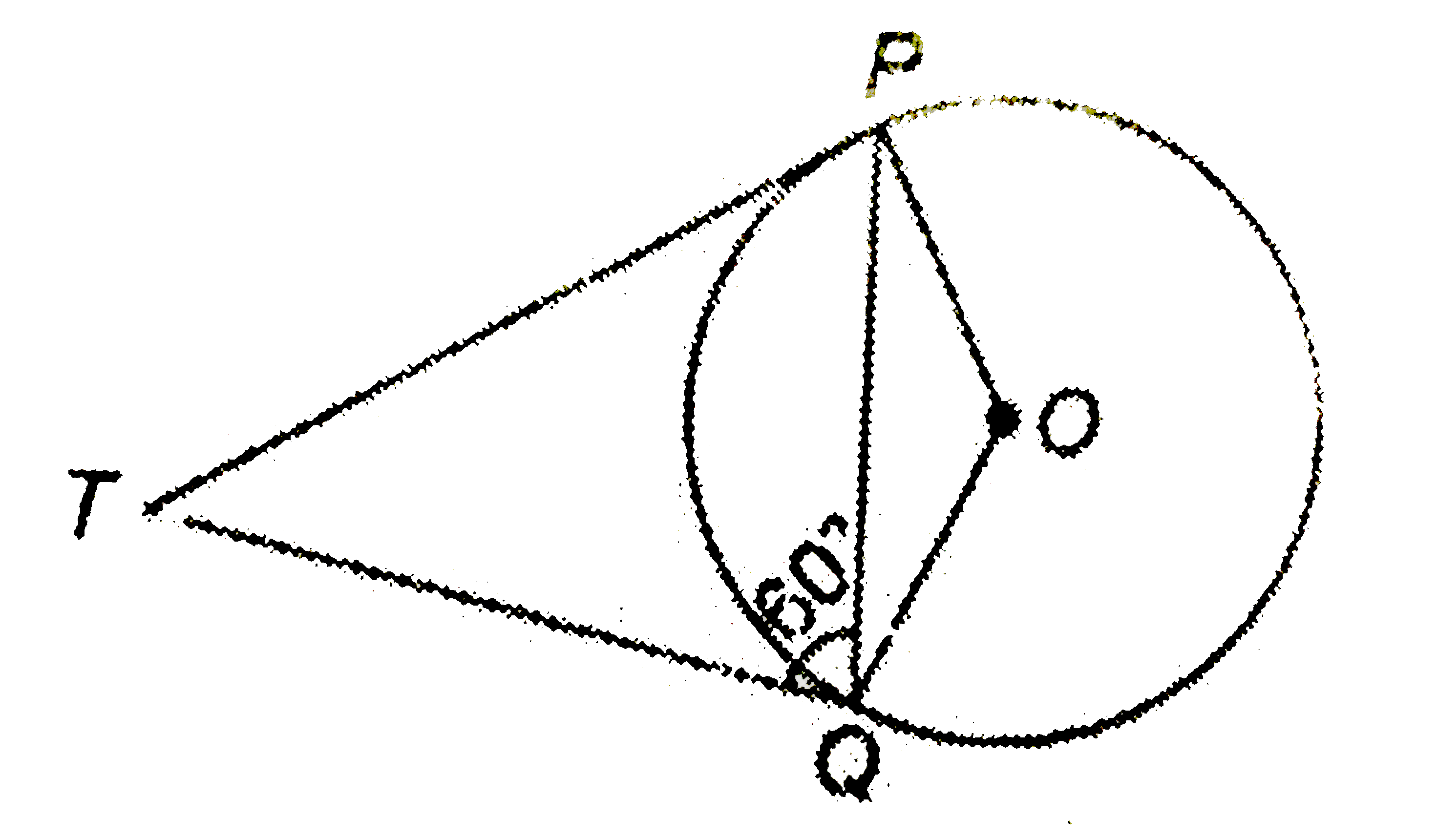
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Video Solution
Text Solution
We know that the tangetns between two tangents from an external point is supplementary to the angle subtended by the radii at the points of contact.
∴∠RPQ+∠ROQ=180∘
⇒∠RQO=180∘−∠RPQ=180∘−30∘=150∘
Now, ∠RSQ=12∠ROQ=12×150∘=75∘ [∵ the angle subtended by an arc at the centre is twice the angle subtended on the remaining part of the circle].
∴∠SQM=∠RSQ=75∘ [alternate int. since RS∣∣PQ]
Also, ∠PQR=∠RSQ=75∘[ angles in alternate segments].
Now,∠SQM+∠RQS+∠PQR=180∘[ angles on a straight line]
∴∠RQS=180∘−(∠SQM+∠PQR)=180∘−(75∘+75∘)=30∘
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ=30∘. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
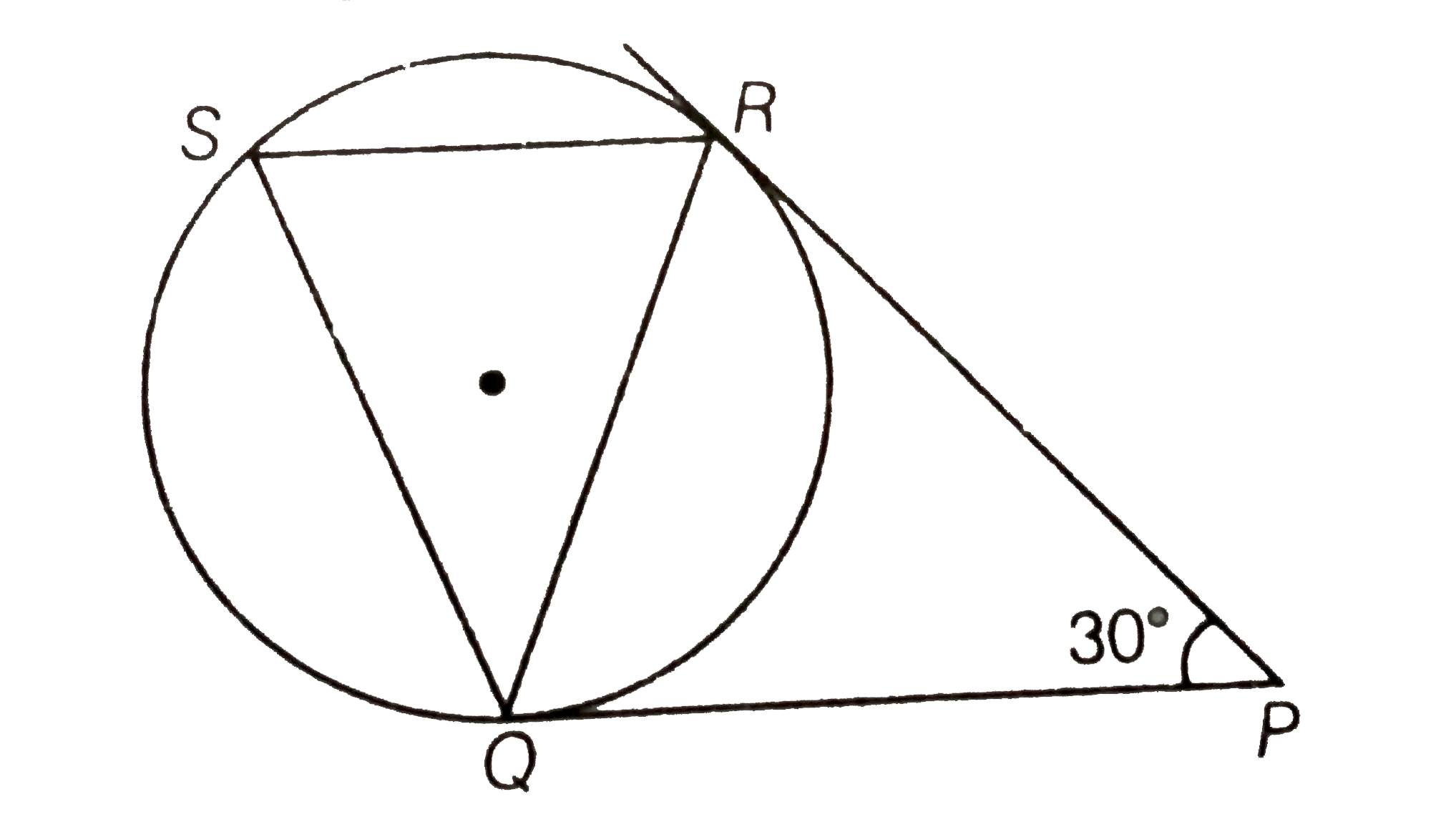 A30∘B40∘C50∘D60∘
A30∘B40∘C50∘D60∘If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘
two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionThe lengths of tangents drawn from an external point to a circle are ________.
View SolutionIn Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
View SolutionThe number of tangents drawn from an external point to a circle is _____________.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View Solution