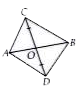
In the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
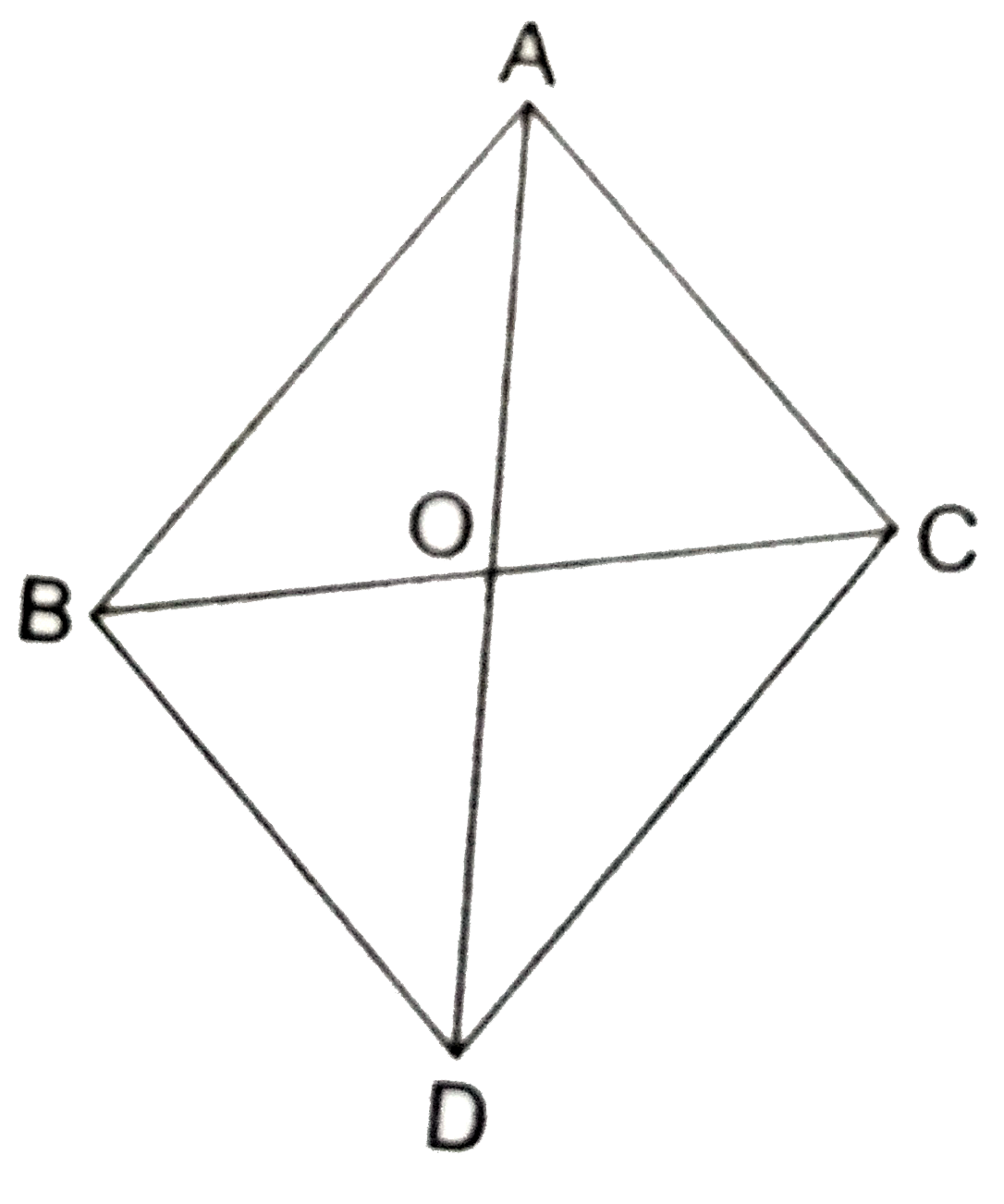
Step by step video & image solution for In the same figure, Delta ABC and Delta DBC are on the same base BC . If AD is intersects BC at O, prove that (ar(Delta ABC))/(ar (Delta DBC))=(AO)/(DO) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT -2 IV. ( LONG ANSWER TYPE QUESTIONS )
3 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT -2 VI. ( CASE STUDY BASED QUESTIONS )
15 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT -2 II. ( SHORT ANSWER TYPE QUESTIONS -I )
3 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
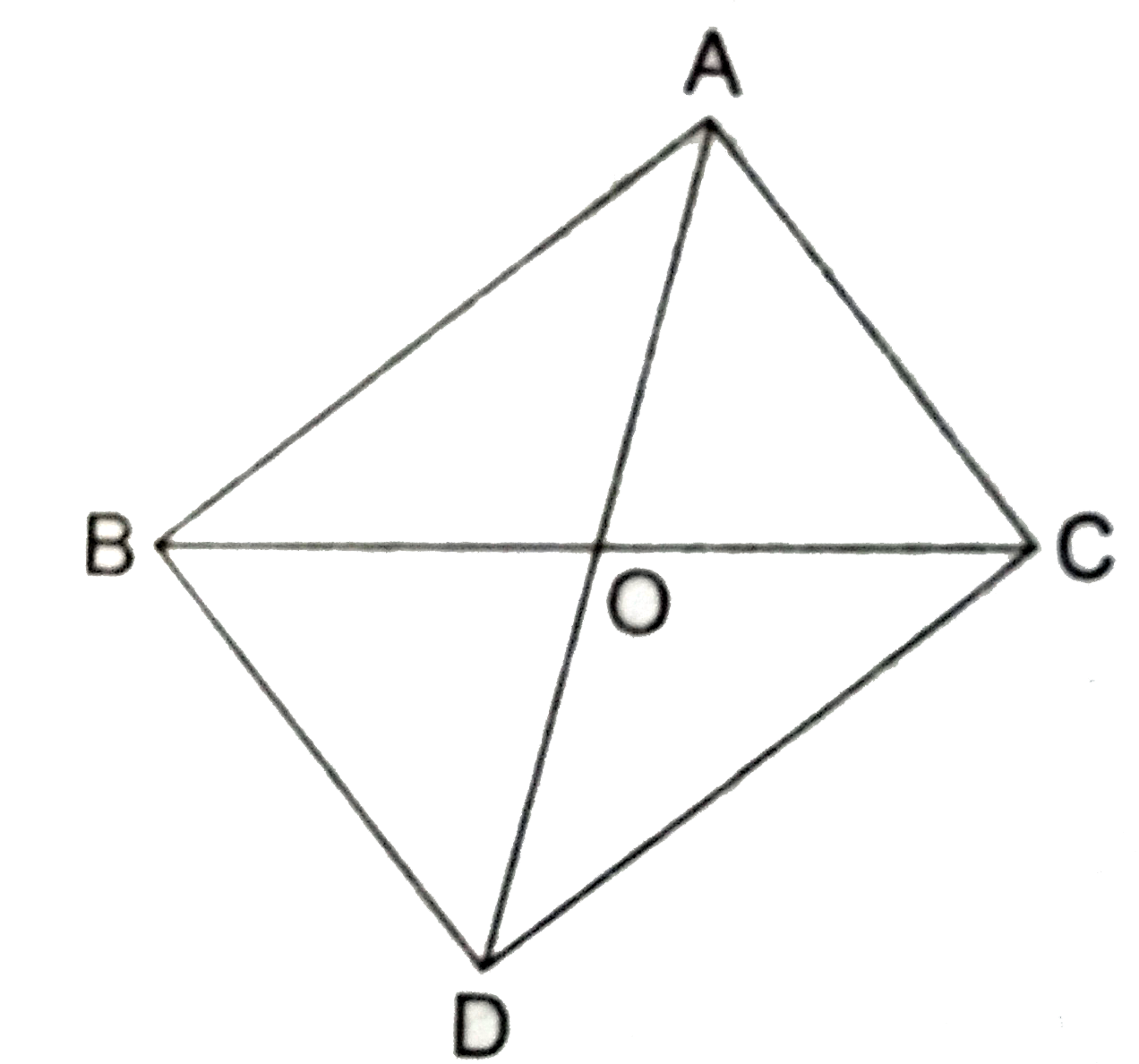
In the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
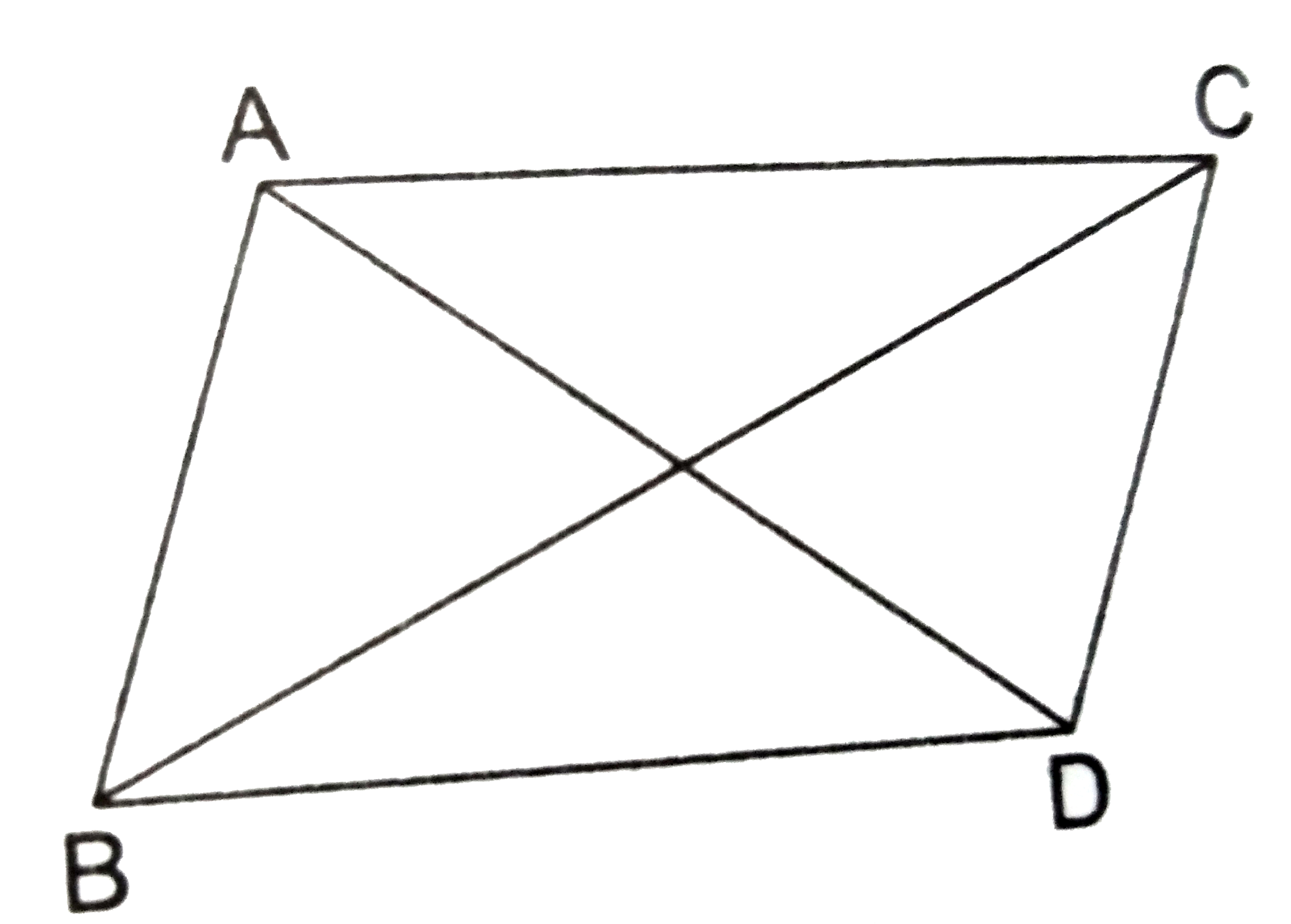
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
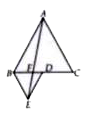
ar(ΔABC) = 2 ar(ΔBEC)
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionIn figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View Solution
