In ABC, AD is a median. Prove that AB + AC 2AD
To prove that AB+AC>2AD in triangle ABC where AD is a median, we can follow these steps:
1. Draw Triangle ABC:
Start by sketching triangle ABC with points A, B, and C.
Hint: Remember that a median connects a vertex to the midpoint of the opposite side.
2. Identify the Median:
Draw the median AD from vertex A to the midpoint D of side BC.
Hint: The point D divides BC into two equal segments, BD and DC.
3. Extend the Median:
Extend AD to point E such that AD=DE. This means DE is also equal in length to AD.
Hint: This construction helps create a new triangle EDC that will be useful for comparison.
4. Join Points:
Connect point C to point E by drawing line segment CE.
Hint: This connection will help us analyze the triangles formed.
5. Analyze Triangles:
Consider triangles ADB and EDC. We have:
- AD=DE (by construction)
- BD=DC (since D is the midpoint)
- ∠ADB=∠EDC (vertically opposite angles)
Hint: Use the properties of congruent triangles to establish relationships between their sides.
6. Apply Congruence:
By the Side-Angle-Side (SAS) criterion, triangles ADB and EDC are congruent. Therefore, we can conclude that:
AB=EC
Hint: Congruent triangles have corresponding sides that are equal.
7. Use Triangle Inequality:
In triangle AEC, apply the triangle inequality:
AC+EC>AE
Substituting EC with AB gives:
AC+AB>AE
Hint: The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
8. Substitute AE:
Since AE=AD+DE=AD+AD=2AD, we can rewrite the inequality:
AB+AC>2AD
Hint: This step connects our earlier results to the original statement we wanted to prove.
9. Conclusion:
We have shown that:
AB+AC>2AD
Thus, the statement is proven.
Hint: Always summarize your findings to reinforce the conclusion of your proof.
Start by sketching triangle ABC with points A, B, and C.
Draw the median AD from vertex A to the midpoint D of side BC.
Extend AD to point E such that AD=DE. This means DE is also equal in length to AD.
Connect point C to point E by drawing line segment CE.
Consider triangles ADB and EDC. We have:
- AD=DE (by construction)
- BD=DC (since D is the midpoint)
- ∠ADB=∠EDC (vertically opposite angles)
By the Side-Angle-Side (SAS) criterion, triangles ADB and EDC are congruent. Therefore, we can conclude that:
AB=EC
In triangle AEC, apply the triangle inequality:
AC+EC>AE
Substituting EC with AB gives:
AC+AB>AE
Since AE=AD+DE=AD+AD=2AD, we can rewrite the inequality:
AB+AC>2AD
We have shown that:
AB+AC>2AD
Thus, the statement is proven.
Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - MULTIPLE CHOICE QUESTIONS
15 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
In a triangle ABC, AD is the median through A and E is the midpoint of AD, and BE produced meets AC at F. Then AF is equal to
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
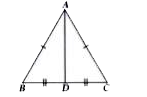 Prove that:
Prove that:
∠BAD=∠CAD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
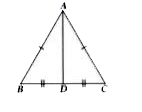 Prove that:
Prove that:
ΔADB≅ΔADC
View SolutionIn a △ABC, AD is the median drawn on the side BC is produced to E such that AD=ED. prove that ABEC is a parallelograms.
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
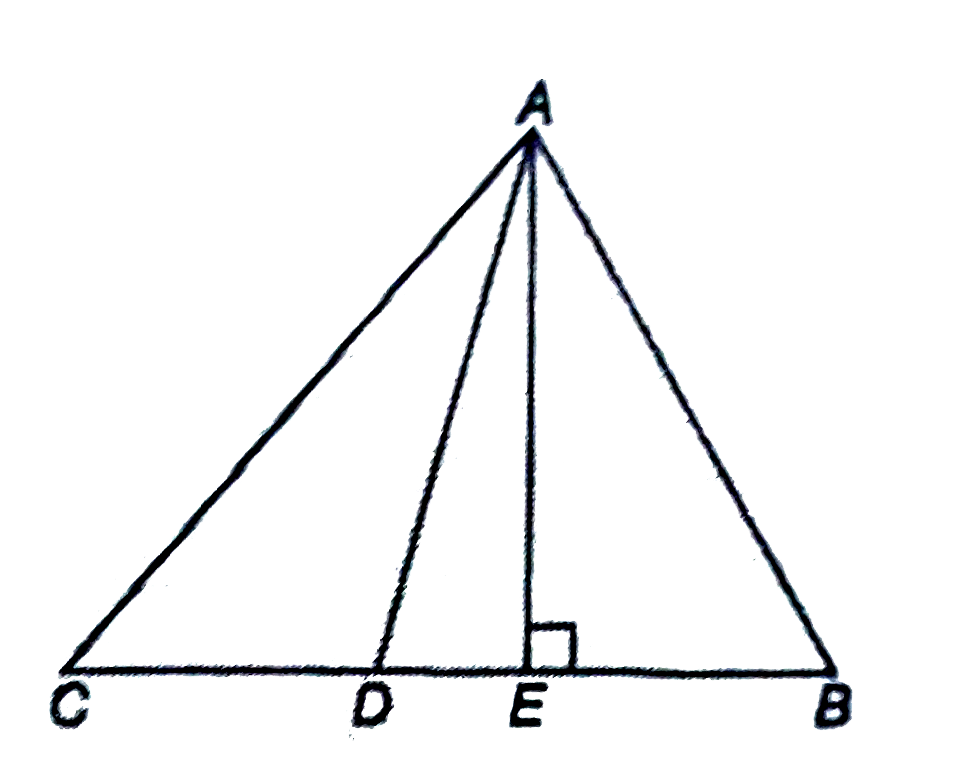
View SolutionA(7, -3), B(5, 3) and C(3, -1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
View SolutionIn Figure, AD is the median and DEAB. Prove that BE is the median.
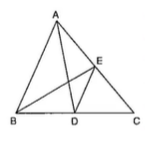
View Solution
