In which of the following figures, you find two polygons on the same base and between the same parallels?
The correct Answer is:D
To solve the question of identifying which figure contains two polygons on the same base and between the same parallels, we can follow these steps:
Step 1: Understand the Definitions
- Same Base: Two polygons are said to be on the same base if they share a common line segment as their base.
- Between the Same Parallels: Two polygons are said to be between the same parallels if both are enclosed by two parallel lines.
Step 2: Analyze Each Figure
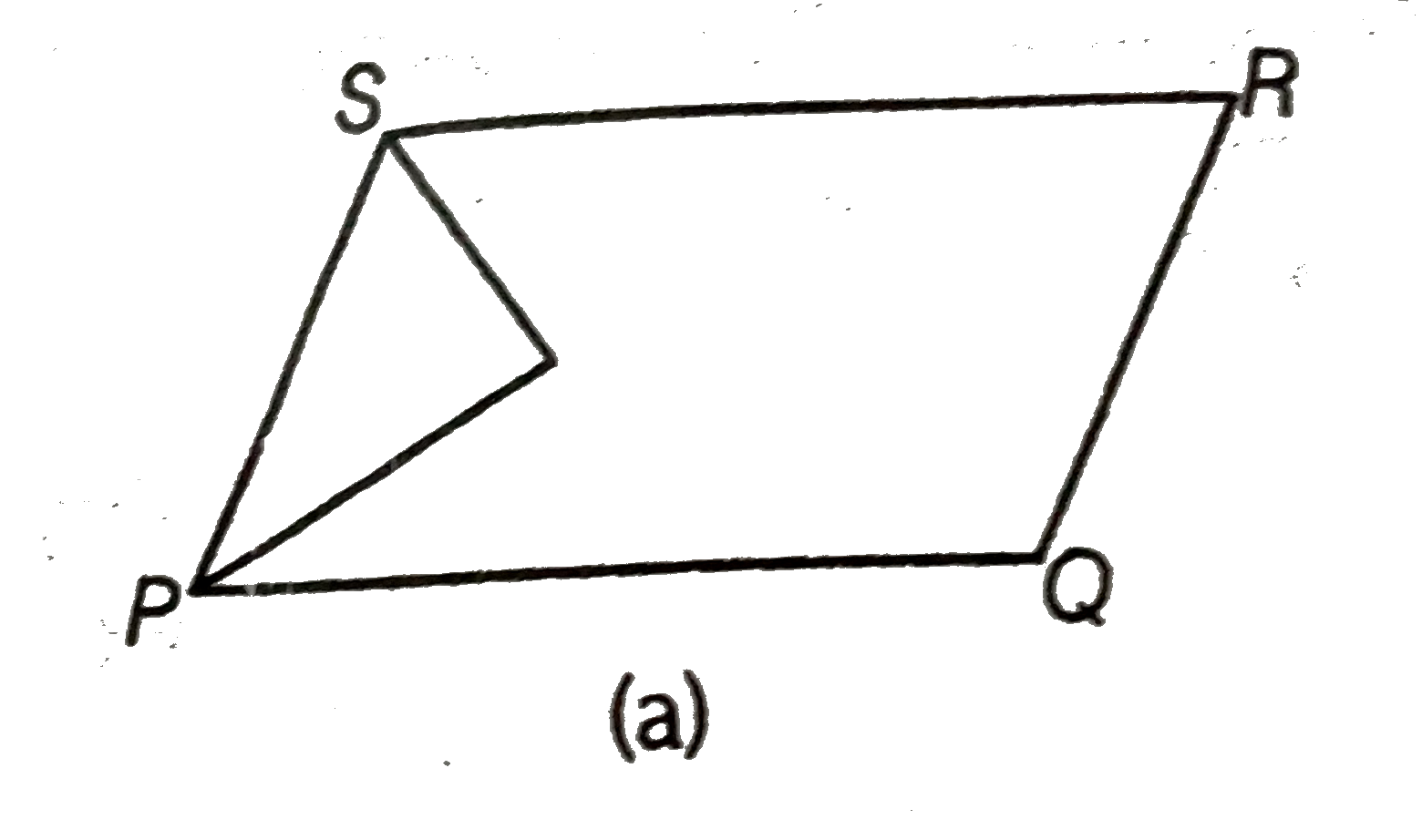
- Figure A: Check if both polygons share a common base and if they are enclosed by two parallel lines.
- Observation: They have the same base but are not between the same parallels.
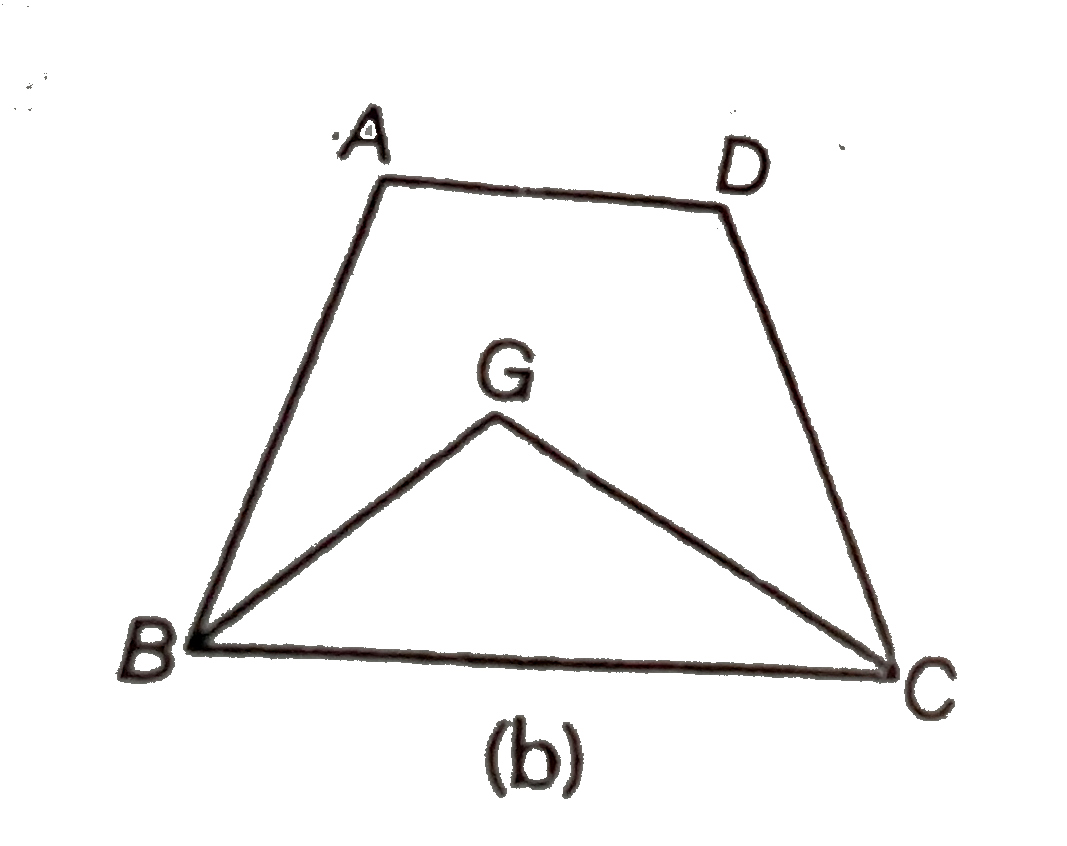
- Figure B: Again, check for the same base and parallel lines.
- Observation: The triangle and quadrilateral share a base but are not between the same parallels.
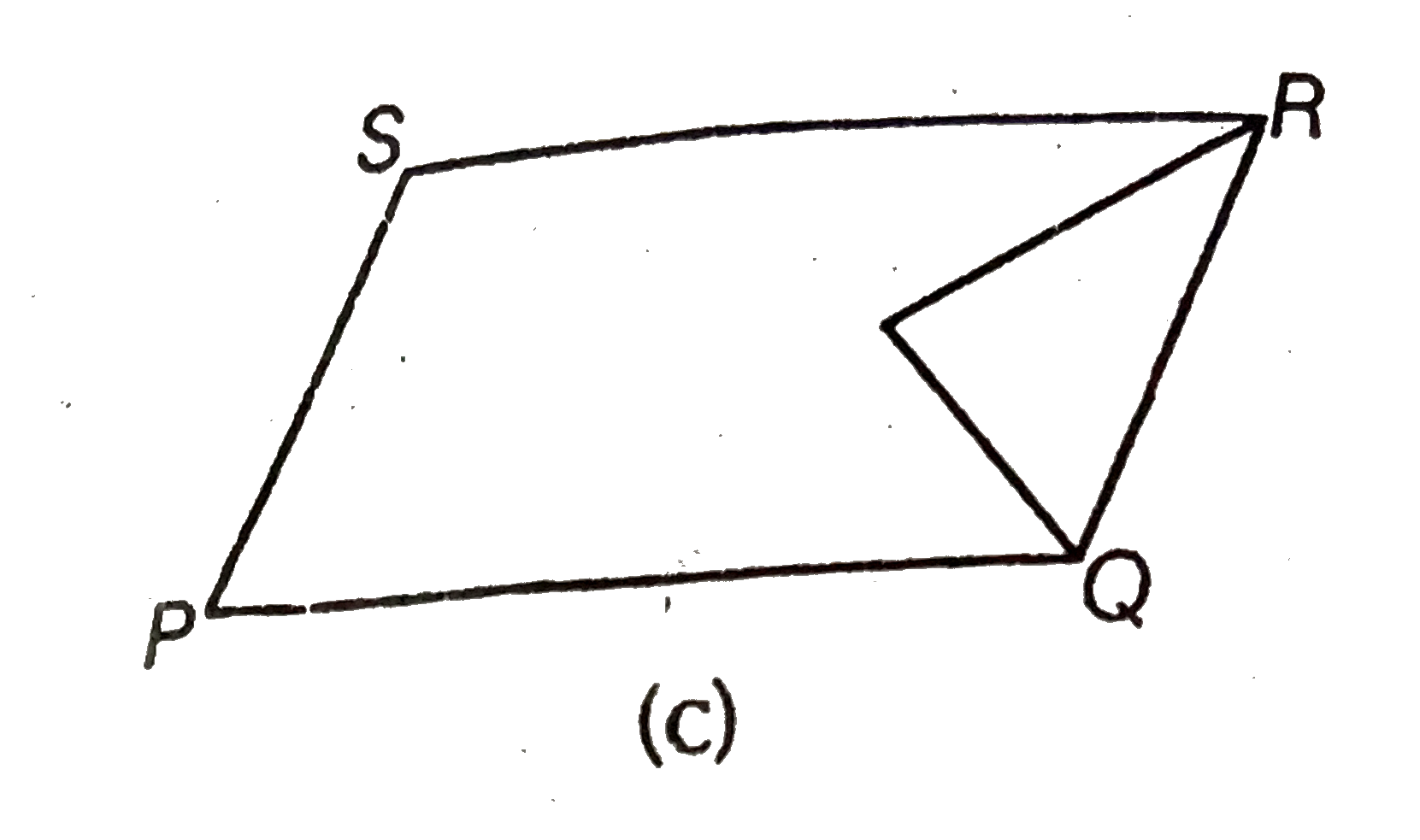
- Figure C: Repeat the analysis.
- Observation: The triangle and quadrilateral share a base but are not between the same parallels.
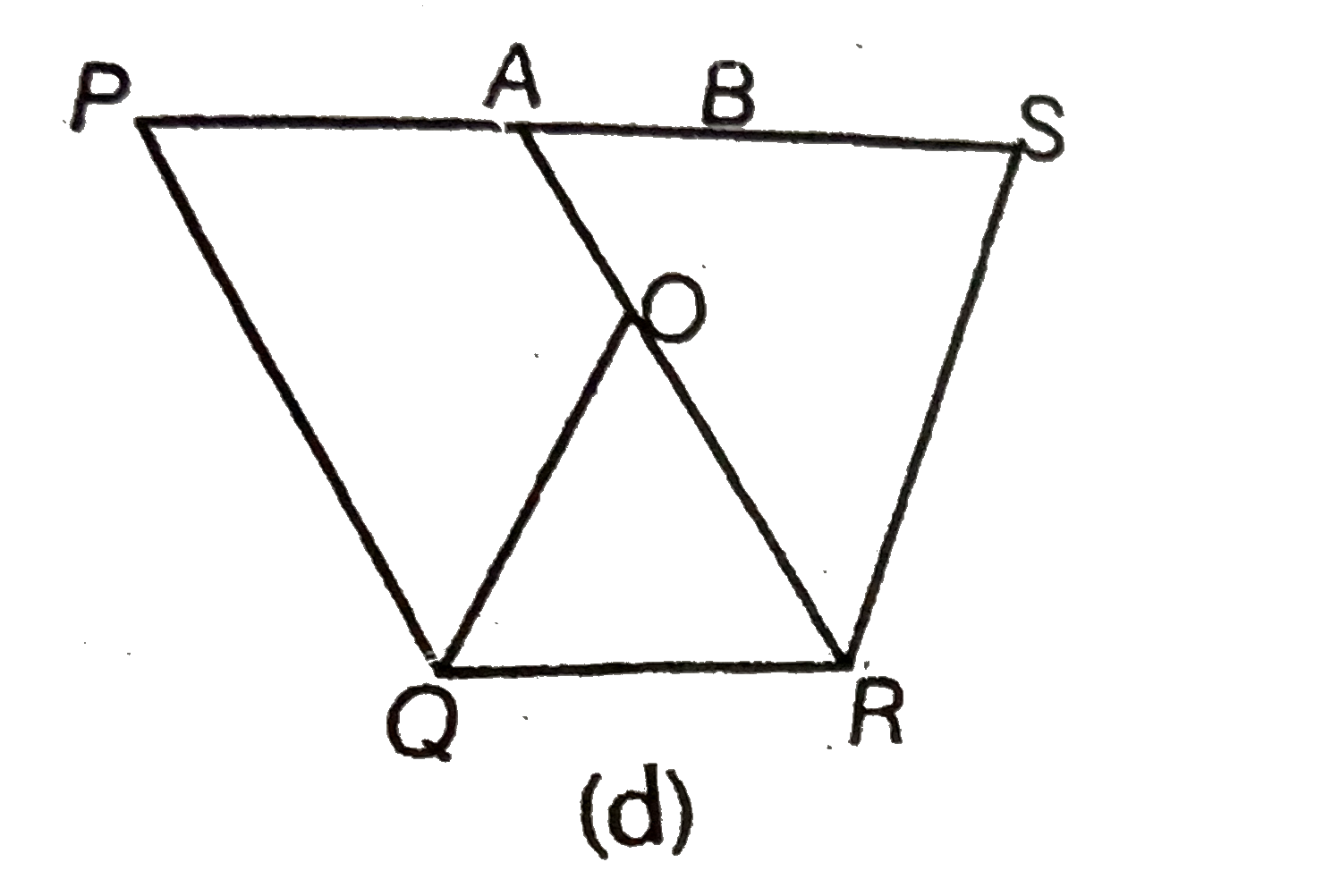
- Figure D: Finally, check this figure.
- Observation: The quadrilaterals share the base QR and are between the same parallel lines PS and QR.
Step 3: Conclusion
After analyzing all figures, we find that only in Figure D do the two polygons (quadrilateral PAQR and quadrilateral BQRS) share the same base QR and are between the same parallel lines PS and QR.
Thus, the answer is Figure D.
---
- Same Base: Two polygons are said to be on the same base if they share a common line segment as their base.
- Between the Same Parallels: Two polygons are said to be between the same parallels if both are enclosed by two parallel lines.
- Figure A: Check if both polygons share a common base and if they are enclosed by two parallel lines.
- Observation: They have the same base but are not between the same parallels.
- Figure B: Again, check for the same base and parallel lines.
- Observation: The triangle and quadrilateral share a base but are not between the same parallels.
- Observation: The triangle and quadrilateral share a base but are not between the same parallels.
- Observation: The quadrilaterals share the base QR and are between the same parallel lines PS and QR.
After analyzing all figures, we find that only in Figure D do the two polygons (quadrilateral PAQR and quadrilateral BQRS) share the same base QR and are between the same parallel lines PS and QR.
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions
5 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.3 Short Answer Type Questions
9 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
Similar Questions
Triangles on the same base and between the same parallels are equal in area.
View SolutionWhich of the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels: Figure (ii) Figure (iii) Figure Figure (ii) Figure (iii) Figure
View Solution
Knowledge Check
Which of the following combinations have the same equivalent resistance between X and Y ?
A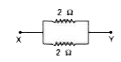 B
B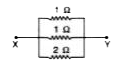 C
C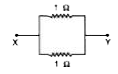 D
D
Which hof the following figures are polygons ?

View SolutionProve that Parallelograms on the same base and between the same parallels are equal in area.
View SolutionProve that two triangles having the same base and equal areas lie between the same parallels.
View SolutionUsing vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionIf a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
View SolutionIf a triangle and a parallelogram are on the same base and between the same parallels lines, then the area of the triangle is equal to half that of the parallelogram. GIVEN : A △ABCand∣∣gmBCDE on the same base BC and between the same parallels BCandAD. TO PROVE : ar(△ABC)=1/2 ar(∣∣gmBCDE) CONSTRUCTION : Draw AL ⊥ BC and DM⊥BC, produced at M.
View SolutionWhich of the following have same significant figures?
View Solution
